On 7 January 2016 a “new” large prime number was discovered, with more than 22 million digits. Time for a blog about these numbers, which have fascinated mathematicians from Greek antiquity until present times.
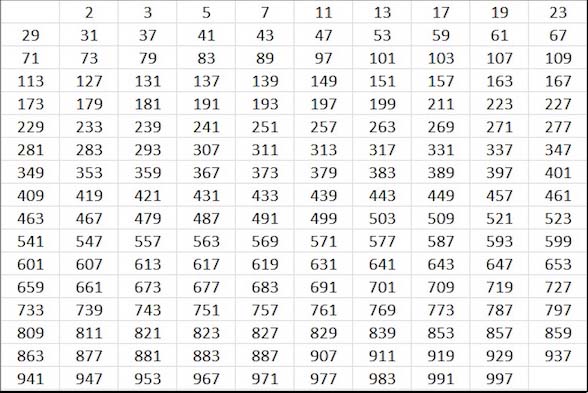
Prime numbers are numbers that can only be divided by 1 and itself. For example 7 is a prime number, but 6 is not because it can be divided by 2 and 3. . Here is a list of the 168 prime numbers smaller than 1000. The number 2 is the only even prime, all others are odd.
How many prime numbers are there?

Euclides, the famous Greek mathematician, living in present-day Egypt around 300 BC, already proved that their number is infinite, and his proof is so elementary, that I often presented it to my students when I was a teacher, as an example of what is called Reductio ad Absurdum.
Euclides’ proof: Assume that you have a complete list of all prime numbers.
- Multiply them together and add 1. Call this number X.
- Because of the added 1, this number X can not be divided by any prime number in your list (there will always be a reminder 1)!
- So there are only two possibilities, either X is prime itself, or it can be divided by a prime number outside your list. In both cases it shows your list was incomplete.
- Therefore our assumption was wrong and the list of prime numbers is infinite!
How to find out if a number X is prime? Do we have to check whether X is divisible by any number, smaller than X ? That would be a tedious job. Fortunately it is not as bad as that…:-). Because it is easy to see that we only have to check whether X is divisible by any prime number, smaller than the square root of X.
For example X=283, is it prime? The square root of 283 = 16.82…, so we have only to check division by 2,3,5,7,11 and 13.
- 283 / 2 = 141 rest 1
- 283 / 3 = 94 rest 1
- 283 / 5 = 56 rest 3
- 283 / 7 = 40 rest 3
- 283 / 11 = 25 rest 8
- 283 / 13 = 21 rest 10
So 283 is a prime number!
This procedure is called Trial Division. For large numbers it becomes time consuming. For example, we want to check if 1000.003 is prime. There are 168 prime numbers smaller than 1000, so we have to do 168 divisions to finally conclude that, yes, 1000.003 is prime. Repeating this procedure for 999.997, you will find that this number is not prime, it can be divided by 757.
Imagine that you have to do these divisions with only pen and paper!
Back to the recently discovered large mega-prime. It is a so-called Mersenne prime, one less than a power of 2: Mp = 2p − 1 with p itself a prime number.
- M2 = 22 − 1 = 4 – 1 = 3 prime!
- M3 = 23 − 1 = 8 – 1 = 7 prime!
- M5 = 25 − 1 = 32 – 1 = 31 prime!
- M7 = 27 − 1 = 128 – 1 = 127 prime!
Could this be a rule to create prime numbers? Unfortunately that is not the case. M11 = 211 − 1 = 2048 – 1 = 2047 = 23 * 89 , not prime!
However the next one M13 = 213 − 1 = 8192 – 1 = 8191 is again prime.
As are M17 = 131.071 and M19 = 524.287. The last two are already quite large, in 1588 the Italian mathematician Cataldi had proven by trial division that they were prime.
Why are these numbers called Mersenne primes?

Marin Mersenne was a French priest with an interest in mathematics, theology and philosophy.
He published in 1644 a list of these numbers 2p − 1, stating that they were prime for p = 2, 3, 5, 7, 13, 17, 19, 31, 67, 127 and 257, and not for any other p below 257.
His list was incomplete and incorrect, but still these prime numbers carry his name…:-)
Incorrect, because M67 and M257 are composite
Incomplete, because M61 , M89 and M107 are prime
Mersenne was correct that M31 = 2.147.483.647 is prime, but how could he know? This is a big number, the square root is ~ 46.340, so he should first determine all prime numbers smaller than 46.340 (there are 4792) and then perform trial division for all those 4792 numbers. It must have been a lucky guess. And certainly it was a guess for M127 = 170.141.183.460.469.231.731.687.303.715.884.105.727 🙂

It was only in 1772, more than a century later, that the great mathematician Leonhard Euler proved the primality of M31.
By a clever analysis of the general structure of Mersenne numbers, he managed to reduce the number of trial divisions to 84 !
Still a big job (pen and paper), the story is that he had a team of helpers to do the actual calculations.
This was the last result using trial division. For more than a century no developments regarding Mersenne primes took place.

Until 1857, when Édouard Lucas, a young French boy (15 years old), gets interested to prove that M127 is prime.
As trial division is not feasible for these large numbers, he studies the structure of the Mersenne numbers and develops a method to check the primality without trial divisions.
After 19 (!) years of testing his methods, he is convinced and announces in 1876 that M127 is prime. The 9th Mersenne prime!
His approach, later refined by others, is still used in the search for new Mersenne primes. Characteristic for this Lucas–Lehmer primality test is that it can decide that a Mersenne number is NOT prime, without finding the factors of this number. For example, using this test, we find that M257 = 231.584.178.474.632.390.847.141.970.017.375.815.706.539.969.331.281.128.078.915.168.015.826.259.279.871 is composite, but we don’t know its factors…:-)
With Lucas’ method, in the following years/decades the primality of M61 , M89 and M107 is proven. Still using pen and paper!
New activity starts only in the 20th century when the first computers are built.

One of them is the famous SWAC computer, built in 1950. Nowadays a PC or even a tablet would be more powerful.
In 1952 it was used to check new Mersenne primes. Within one year 5 new ones were found, for p = 521, 607, 1279, 2203 and 2281. Still using the methods developed by Lucas
Very large numbers! Here is prime number M2281 with 687 digits. To make it more readable, spaces have been inserted after three digits.
446 087 557 183 758 429 571 151 706 402 101 809 886 208 632 412 859 901 111 991 219 963 404 685 792 820 473 369 112 545 269 003 989 026 153 245 931 124 316 702 395 758 705 693 679 364 790 903 497 461 147 071 065 254 193 353 938 124 978 226 307 947 312 410 798 874 869 040 070 279 328 428 810 311 754 844 108 094 878 252 494 866 760 969 586 998 128 982 645 877 596 028 979 171 536 962 503 068 429 617 331 702 184 750 324 583 009 171 832 104 916 050 157 628 886 606 372 145 501 702 225 925 125 224 076 829 605 427 173 573 964 812 995 250 569 412 480 720 738 476 855 293 681 666 712 844 831 190 877 620 606 786 663 862 190 240 118 570 736 831 901 886 479 225 810 414 714 078 935 386 562 497 968 178 729 127 629 594 924 411 960 961 386 713 946 279 899 275 006 954 917 139 758 796 061 223 803 393 537 381 034 666 494 402 951 052 059 047 968 693 255 388 647 930 440 925 104 186 817 009 640 171 764 133 172 418 132 836 351

Computers became more powerful, and new Mersenne primes were discovered. In 1961 the first Mersenne prime with more than 1000 digits was found, M4253, using an IBM 7090 mainframe computer (pic left)
And in 1979 the first Mersenne prime with more than 10.000 digits was found, M44.497, using a Cray supercomputer.
You might expect that the recently discovered Mersenne prime M74.207.281 with more than 22 million digits has been found using a super-super computer…:-) But that is not the case! Actually PC’s were used, not one but many, working together!
In 1996 the Great Internet Mersenne Prime Search ( GIMPS) project was started. It is an example of what is called distributed computing. A PC will often be idle, so why not let it work during that time for a project such as GIMPS. Just download some software and your PC will try to find a new Mersenne Prime. Many thousands of volunteers are doing this. And with success
Since 1996, 15 new Mersenne primes have been found, all of them using GIMPS!
Of course finding a new Mersenne prime has no scientific value, it is just an intellectual challenge. But you might win a prize!
When in 1999 the first Mersenne prime was found with more than 1 million digits,M6.972.593 , the Electronic Frontier Foundation awarded this result with a prize of 50.000 US$. In 2008 M37.156.667 was found, with more than 10 million digits. The award was 100.000 US$
Two more prizes have not yet been awarded
- 150.000 US$ to the first individual or group who discovers a prime number with at least 100 million digits
- 250.000 US$ to the first individual or group who discovers a prime number with at least 1 billion digits
The latest Mersenne prime M74.207.281 has 22.338.618 digits, not yet enough for the next reward
So, why not join GIMPS! I did….:-)
For this blog I have made extensive use of The Prime Pages
Large numbers have been calculated using the Online Big Number Calculator