I could have named this blog Uniform Polyhedrons, but I think in that case not many would have read it 😉 A polyhedron is a 3D object, bounded by polygons and a polygon is a flat surface, boudned by straight lines. A cube is a simple polyhedron and a triangle is a simple polygon.MOre terminology in the appendix.

When I was a kid, I was fond of making cardboard models of buildings, ships etc. I bought the “bouwplaten” in the local bookstore. It was quite a popular pastime in those days, now no more. Here are two simple examples, found on the Internet.

It was during the 1970s , on a trip to London, that I came across the book Polyhedron models by Magnus Wenninger. It contained descriptions of 119 polyhedrons with detailed instructions how to make cardboard models of them. With my youthly love of bouwplaten and my interest in mathematics I immediately bought the book. Left my copy, right Magnus Wenninger (1919-2017) with a complicated polyhedron in his hands.

Back home, I bought sheets of colored cardboard and started building polyhedrons. Compared with the commercial “bouwplaten” as shown above, where you just have to cut out he various pieces, you have to draw the pieces first on the cardboard sheet, add tabs and then only cut them out. Here are two examples. The numbers are from Wenninger’s book, which can be found online.

The tetrahedron (left)is the most simple polyhedron, it consists of just four triangles. I have marked how many pieces you have to cut with a colored number. The football like polyhedron with the unspeakable name (right) consists of 30 squares, 20 hexagons and 12 decagons. 62 pieces in total.

Here are a few of the polyhedrons I have built. That was more than 40 years ago, the colors have faded. The polyhedron in the center of the top row is still “simple”, consisting of squares and triangles. The one left on the top row looks more complicated, but when you look carefully, you will see that it only consists of triangles! But only parts of a triangle are visible from the outside. In the right polyhedron, on the bottom row it is easy to see that there are pentagons (five-sided polygon), but there are also hexagons (six-sided polygons), which are hardly visible in this model. In total 12 pentagons and 10 hexagons!.

The polyhedrons where all faces are completely visible, are called convex, the others where you can only see parts of the faces are called nonconvex. See the appendix for more terminology and mathematical details.

Nonconvex polyhedrons are more difficult to build, because you have to be careful that the pieces of one polygon have the same color. But they are worth building, because they are beautiful. Here are a few examples. The left polyhedron consists of 12 pentagons and 12 pentagrams, 24 faces in total. The one at the right is more complicated , 20 triangles, 12 pentagrams and 12 decagons (10-sided polygon), total 44 faces.

Two more. The polyhedron left has 30 squares, 12 pentagons and 12 decagons, total 54 faces. And the beautiful polyhedron to the right has 20 triangles, 30 squares and 12 pentagrams, total 62 faces. The complexity of this polyhedron is difficult to see in a picture. On Wikipedia I found a 3D version which you can rotate with your mouse. Amazing, try it out and see if you can find the triangles (easy) and the squares (difficult).

The polyhedrons at the end of Wenninger’s book are even more complex, Here is a description with templates for the “Great Inverted Retrosnub Icosidodecahedron“. Yes, they all have names, see the appendix. It contains 80 triangles and 12 pentagrams, 92 faces in total .His description starts with “This polyhedron is truly remarkable in its complexity” and at the end he writes “Your patience and perseverance will have to hold out for more than 100 hours if you want a complete model of your own “

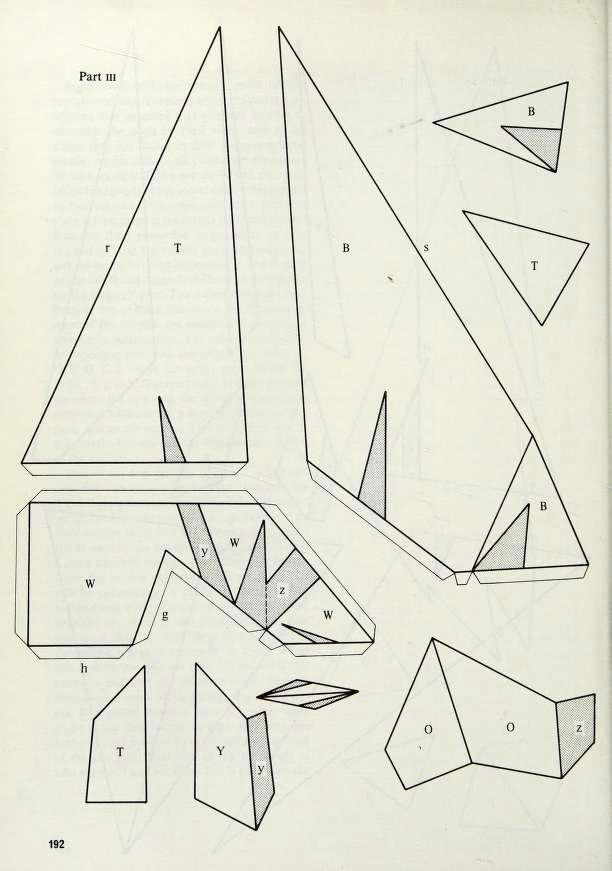
At first I decided that “more than 100 hours” was too much for me. But I was curious about this polyhedron, and I used the templates to build a small part of it.. Soon I found out that there was something wrong with the templates for this model. Parts that had to be glued together, had different lengths! I tried to check and correct the size of the pieces (see right image with my comments) but that did not work..

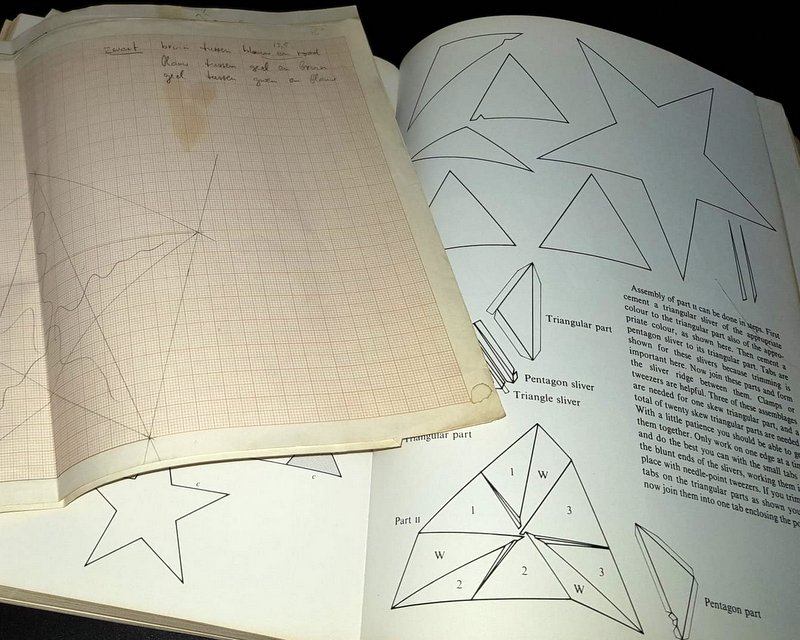
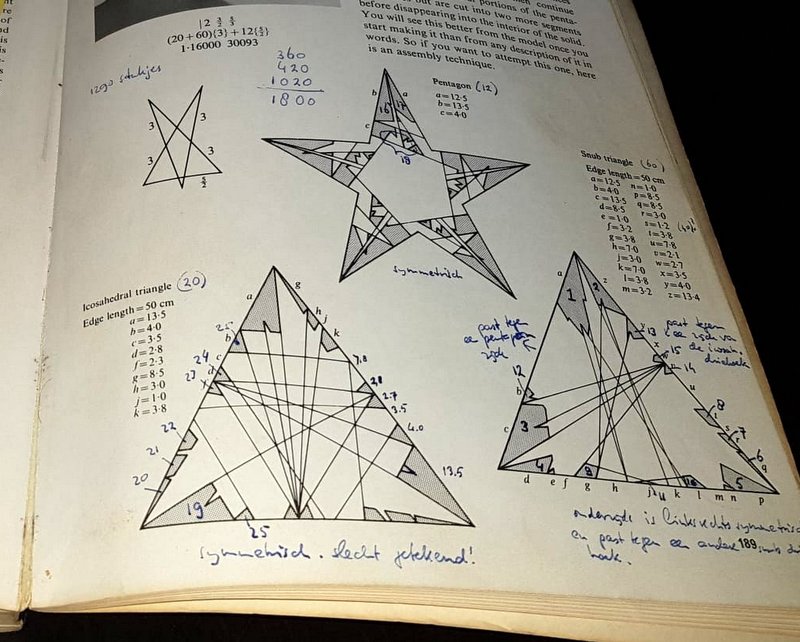
I decided to contact Wenninger, but didn’t have his address, so I wrote to the Cambridge University press ( the publisher), asking them to forward my letter to Wenninger. I didn’t really expect a reply, so I was pleasantly surprised when after a couple of months I got a letter from Wenninger. He explained that in the printing process of the book one or two templates had been incorrectly represented. A few more buyers of the book had noticed the error. His letter contained the correct templates!.

After his kind gesture I felt “morally” obliged to build the polyhedron. I spent many evenings cutting and gluing the 1290(!) pieces. I did not keep track of the hours, but it must have been more than 100. Here is the final result. Of course I took a picture and sent it to Wenninger.

Here is a digital 3D version of the polyhedron. Rotate it with your mouse, to see the complexity.

I assume that in a reprint of the book the mistakes will have been corrected, but when I built the model, it must have been one of the few in the world ;-). Years later I visited the Science Museum in London, where they have the whole collection.

Polyhedrons have fascinated artists, philosophers and mathematicians throughout the ages. Here are Durer;s famous Melencolia I (1514) and John Cornu’s Melencolia (2011)

Appendix

First some terminology.

• A polygon is a 2D figure with straight sides, for example a triangle. When all sides are equal it is called a regular polygon
• A polyhedron is a 3D form bounded by polygons, for example a cube. A polyhedron has faces, edges and vertices (plural of vertex) When the polygons are regular and all vertices similar, the polyhedron is called uniform.

The left polyhedron has 6 faces (F=6), 12 edges (E=12) and 8 vertices (V=8). The right polyhedron has F=4, E=6 and V=4.

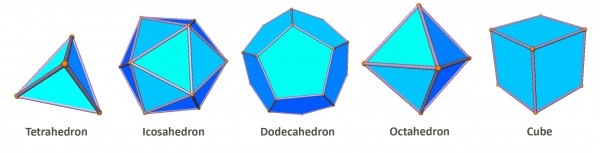
The most simple polyhedrons were already known in antiquity and are called Platonic solids. These polyhedrons have only one regular polygon as face. , a triangle, square or pentagon. Here they are

There are 13 polyhedrons that have more than more than one regular polygon as face.. They are called Archimedean solids, because they were first enumerated by Archimedes, later rediscovered by Kepler who gave them their names. Here they are. Notice that they all have one single edge.

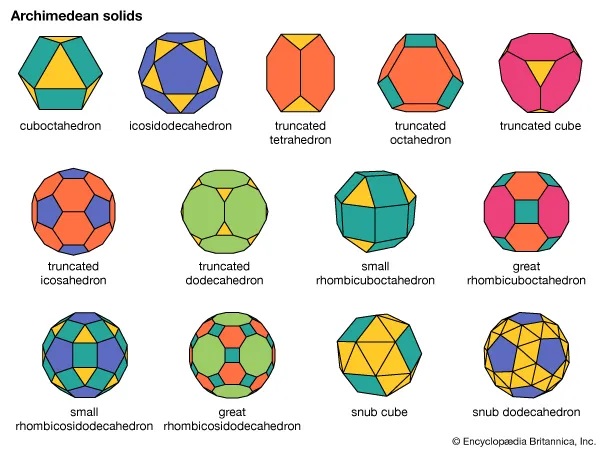
The names give information about the composition of the polyhedron. For example the icosidodecahedron has 20 (icosi) triangles and 12 (dodeca) pentagons.

The polyhedrons often contain pentagrams. A pentagram is related to a pentagon by a process called stellation, extending the sides of a polygon. Polyhedrons can also be stellated by extending their faces. Left the pentagram and right one of the stellated dodecahedrons.(there are three more)

In the Platonic and Archimedean polyhedrons all faces are completely visible, The mathematical term is that these polyhedrons are convex. The stellated dodecahedron, shown above, has pentagrams as faces, but the center part of the pentagram is not visible, it is inside the polyhedron. The mathematical term is that this polyhedron is nonconvex. In total 53 nonconvex polyhedrons exist. This has been proven only in 1970.

Wenninger’s book describes 119 uniform polyhedrons, the 5 platonic solids, the 13 Archimedean ones, 48 polyhedron stellations and the 53 nonconvex polyhedrons. A List of Wenninger polyhedron models can be found on Wikipedia. The list contains images of all polyhedrons and lots of details

Here are the numbers of the polyhedrons shown in this blog (I have built more). 17, 24, 39, 76. 80, 99, 102, 105, 107 and 117.Except 39, a stellation of the icosahedron, they all have a Wikipedia page.

When I built my models, PC’s were still in an infant stage and the World Wide Web did not yet exist. Nowadays there is wealth of information available, there even exists software to create the polyhedrons digitally. Great Stella looks promising. I feel tempted 😉

Why did I write this blog, more than forty year later? Recently I visited the Bellevue Hotel in Penang. The owner of the hotel is a friend of mine. In the garden of the hotel he has built a geodesic dome. He was a close friend of the American architect and philosopher Buckminster Fuller (1895-1983), who was the “inventor” of the geodesic dome.

You will not be surprised that there is a close relation with the polyhedron models of Magnus Wenninger. Have a look at the Wikipedia article Geodesic polyhedron, where both Buckminster Fuller and Wenninger are mentioned. Enjoying the view and admiring the dome, the thought arose to write a blog about my “hobby” from the past 😉