Let me start with a rabbit tale..:-)
Once upon a time a pair of rabbits was born. One month later they were mature and mated. After a pregnancy of 1 month, a new pair of rabbits was born (and being rabbits, the parents mated again immediately). In this tale rabbits have eternal life and keep mating. The question is, how does the number of rabbit pairs grow with time?
Let us do some simple arithmetic (if you are afraid of numbers, skip this paragraph)
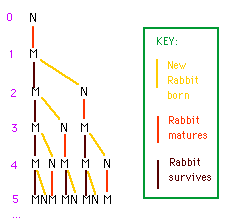
- At the start there is 1 pair, just born. We call it pair A
- After 1 month this pair A is mature and mates, so still 1 pair
- After two months, pair A delivers a new pair B, so we have now 2 pairs
- After three months pair A delivers again a new pair C, pair B has matured and mated, so 3 pairs
- After four months pair A delivers pair D, pair C has matured and mates, but now also pair B produces pair E, so totally 5 pairs
- After five months pair A delivers pair F, pair C delivers pair G, pair B delivers pair H, totally 8 pairs of rabbits.
Complicated..:-)? Maybe the graph below will help. Red vertical lines show mating (M), yellow diagonal ones indicate gestation and delivery (N), black vertical ones are stable (each month producing a new pair)
So the sequence gives (in rabbit pairs) 1,1,2,3,5,8… can you guess how it continues?
Here is the answer, each number is the sum of the two preceding ones! 2+3=5, 3+5=8, so the next term should be 5+8=13, then 8+13=21, 13+21=34. A very simple rule..:-)
Still you may wonder, who came with such a funny story. Well, that was Fibonacci, an Italian mathematician, living from c. 1170 – c. 1250.
The numbers are now called Fibonacci numbers:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765 ...
This Fibonacci series has several remarkable properties. To explain one of them, I first have to introduce the Golden Ratio, also known as the Divine Proportion!
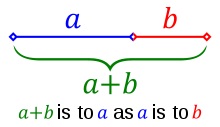
Hm, a little bit more mathematics (skip it if you are afraid of formulas). We have to go back to the old Greek philosophers. They were fascinated with numbers and ratios between numbers. You you may remember the Pythagorean triangles from your school days! Here is one of the problems they were interested in. Suppose you have a stick you like to divide in two parts a and b in such a way that the the ratio (a + b) / a is the same as the ratio a/b
Hm, let’s try. We have a stick of 100 cm long and we divide it in a =50 cm and b = 50 cm. Then (50+50)/50 = 2 and 50/50 = 1. Not at all the same. Next we try a = 60 and b = 40. This results in (60+40)/60 = 1.6666.. and 60/40 = 1.500. Not yet equal. Next a =62 and b =38. Result: (62+38)/62 = 1.6129.. and 62/38 = 1.6315.. Getting closer! Refining this, we finally find a division of a = 61.8034.. and=38.1966.. with a common ratio of 1.6180.. The Greek mathematicians named this ratio the Golden Ratio with φ (phi) as its symbol.
Back to our Fibonacci numbers. Let us take the ratio of two consecutive numbers. We start with 1/1 = 1, then 2/1 = 2, 3/2 = 1.5, 5/3 = 1.666, 8/5 = 1.6, 13/8 = 1.625, 21/13 = 1.615, 34/21 = 1.6190, 55/34 = 1.6176, 89/55 = 1.6182, 144/89 = 1.6180 etc
Surprise! The Fibonacci numbers and the Golden Ratio are related!
The ratio of two consecutive Fibonacci numbers approaches the Golden Ratio !
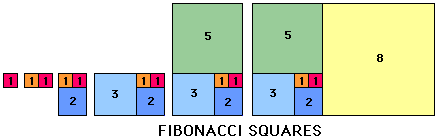
For the second remarkable property we will visualise the Fibonacci numbers in two dimensions, as squares. We add each square so that the result will be a rectangle. The last rectangle in the picture below measures 13 by 8, ratio 13/8 = 1.625, already close to the Golden Ratio..:-)
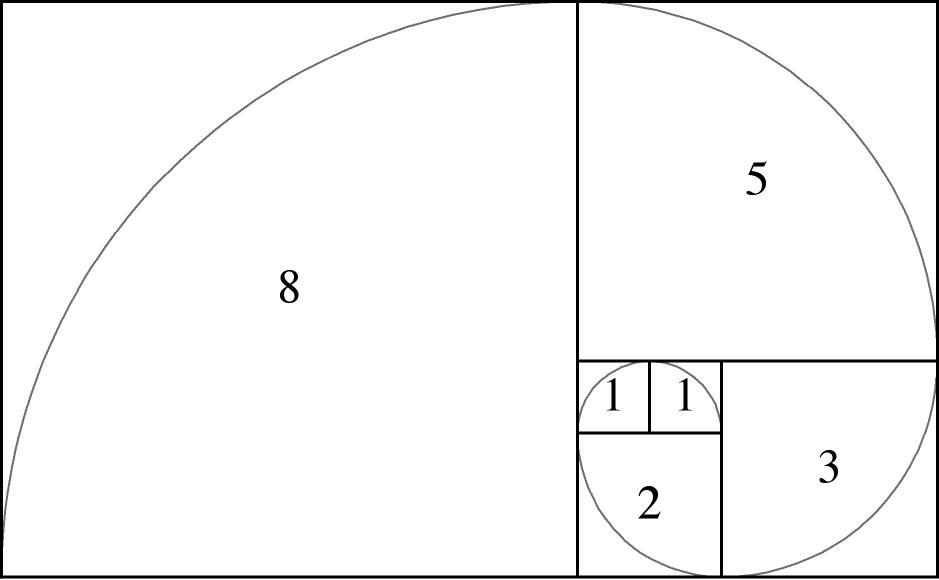
Next step, in each square we draw a quarter-circle. This is the result, we get a beautiful spiral, the Golden Spiral!
Not surprisingly, artists throughout the ages have been fascinated by Fibonacci numbers and the Golden Ratio. And in nature we come across many examples of Golden Spirals.
But that will be the topic of a separate post.
Note for readers with a mathematical background. The spiral above is an approximation of the Golden Spiral. And the Golden Ratio can be easily calculated.
Finally: the Golden Spiral is a special case of a logarithmic spiral, with a growth factor of φ for every 90 degrees of rotation.



I knew a little about Fibonacci numbers, but this is a delightful explanation of them.