Category Archives: Astronomy

Life on Europa & Enceladus?

Posted on by
Reply

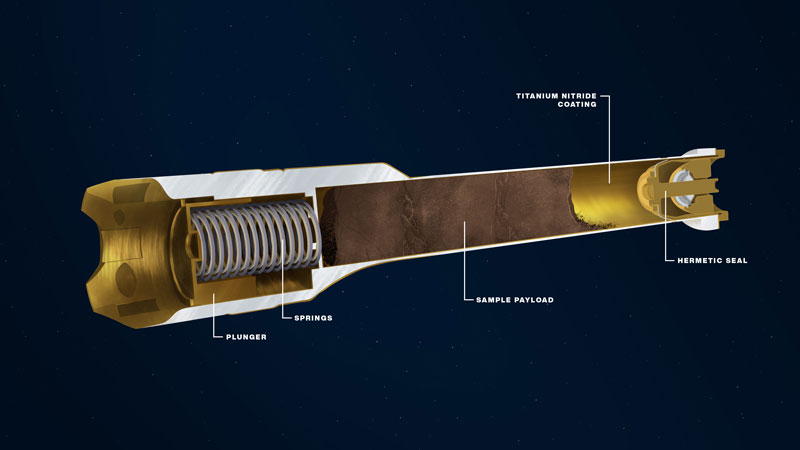
It is generally assumed that you need liquid water for life to develop. The planet Mars is now dry and arid, but had lots of water in its far past.. The Perseverance rover (see my blog) is at the moment collecting samples of Martian soil, hoping to find fossil remains of (microbial) life, until now without results. Disappointing for those who are convinced that “simple” life must be ubiquitous in the universe.

When you have been following my blog, you will know that I am not really surprised. Personally I think that (simple) life will NOT develop easily, even in a suitable environment. See my recent post about the Drake Equation.

Are there other places in our solar system with (abundant) liquid water? Yes, there are, here are two, Europa and Enceladus. Europa is a moon of Jupiter and Enceladus a moon of Saturn. Europa is large with a diameter of 3122 km, only slightly smaller then Earth’s Moon (3475 km). Enceladus is much smaller, with a diameter of 504 km. In this image you see the relative sizes of Earth, Moon and Enceladus,

Here are the two moons, Europa left and Enceladus right.. Both moons are covered with a thick crust of water ice. This ice surface has a temperature of about -200 degree Celsius. But underneath this crust both moons have oceans of liquid water!

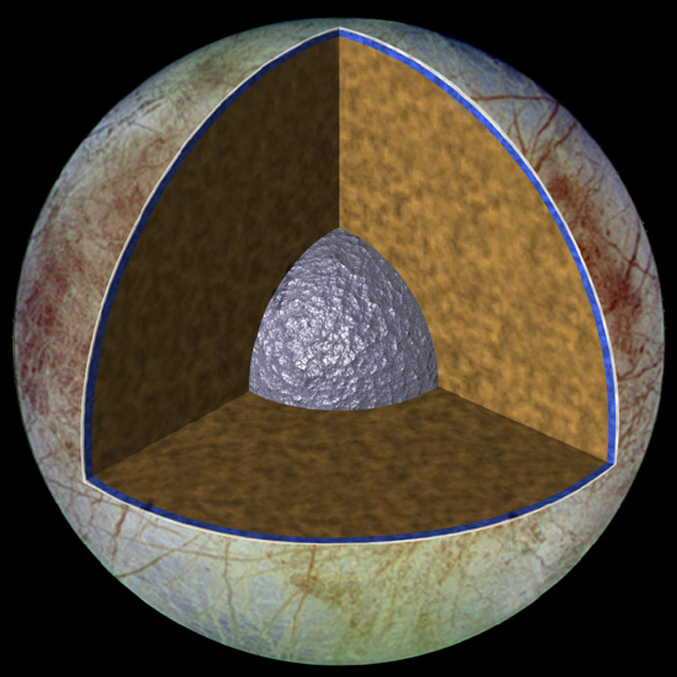
We think that the interior of the two moons look like this. Europa has a metallic core (iron and nickel),a rocky mantle and a (salty) ocean with an estimated depth of 60-150 km.. A thick ice crust ( 15-25 km) covers the ocean. The model shows the layers to scale.

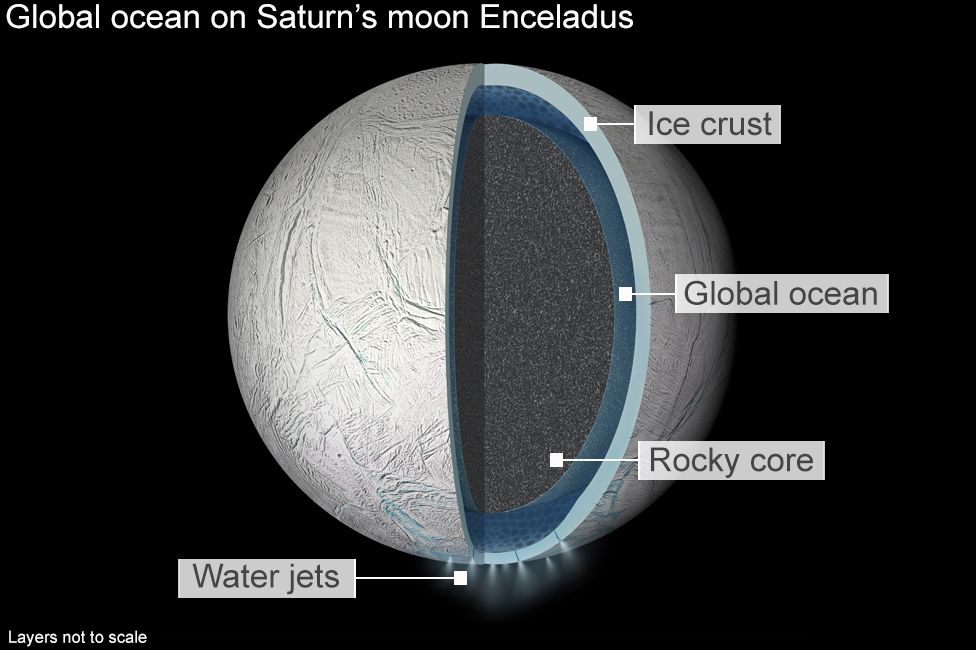
Enceladus has a rocky core with radius of ~ 180 km , covered by a 30 km deep ocean. and a 20 km thick crust. The ice crust is thinner at the south pole.

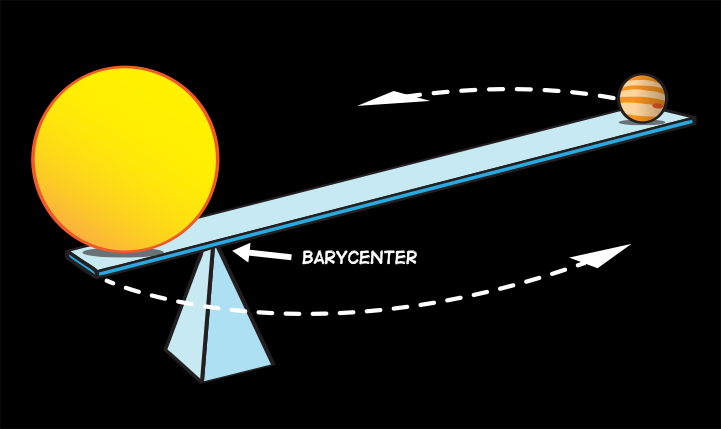
How is it possible that these moons have liquid water under their ice crust? Where does the energy come from, the Sun is far way. The answer is: because of the tidal forces exerted by the giants Jupiter and Saturn on their moons.

Newton’s gravitation between two objects depends on the distance between them. For example the gravitational force exerted by the Moon on Earth is stronger on the side facing the Moon than on the other side. This difference is responsible for the tides. The tidal friction will slow down the rotation of Earth , so the length of a day will increase a little bit, about 1,8 millisecond per century. In the far past when the moon was born, the day length may have been about 4 hours only!, For the moon the story is similar: tidal friction has slowed it down, even a lot more, the Moon shows always the same face to Earth, it is “tidally locked”. Actually all the major moons in the Solar System are tidally locked to their planet.

Even tidally locked moons still can undergo tidal flexing, if the orbit is elliptical, a kind of kneading. Model calculations for Europa and Enceladus indicate that this .can generate enough energy to keep the oceans liquid. More (technical) details here.

So both moons have liquid water and a source of energy , two of the essential ingredients for life as we know it. The third ingredient (chemicals like carbon, hydrogen, nitrogen, oxygen, sulfur, and phosphorus) should be available in the rocky core.

The information about the two moons comes basically from two successful space missions. The Galileo spacecraft arrived at Jupiter in 1995 and stayed in orbit until 2003. It’s main mission was to study the planet, but it managed to have numerous flybys’ of Europa. The Cassini entered Saturn’s orbit in 2004 and stayed there until 2017.

The Cassini mission was very successful, click here for an overview. One of the most spectacular discoveries was that Enceladus is an active moon. There are geysers in the south polar region of the moon! This picture was taken by Cassini in February 2010.

The geysers consist of water vapor and ice particles. The explanation is that water seeps from the ocean floor into the rocky core where it is heated. The heated water rises and erupts though fissures in the icy crust.. It is a bit similar to the hydrothermal vents in Earth’s oceans.

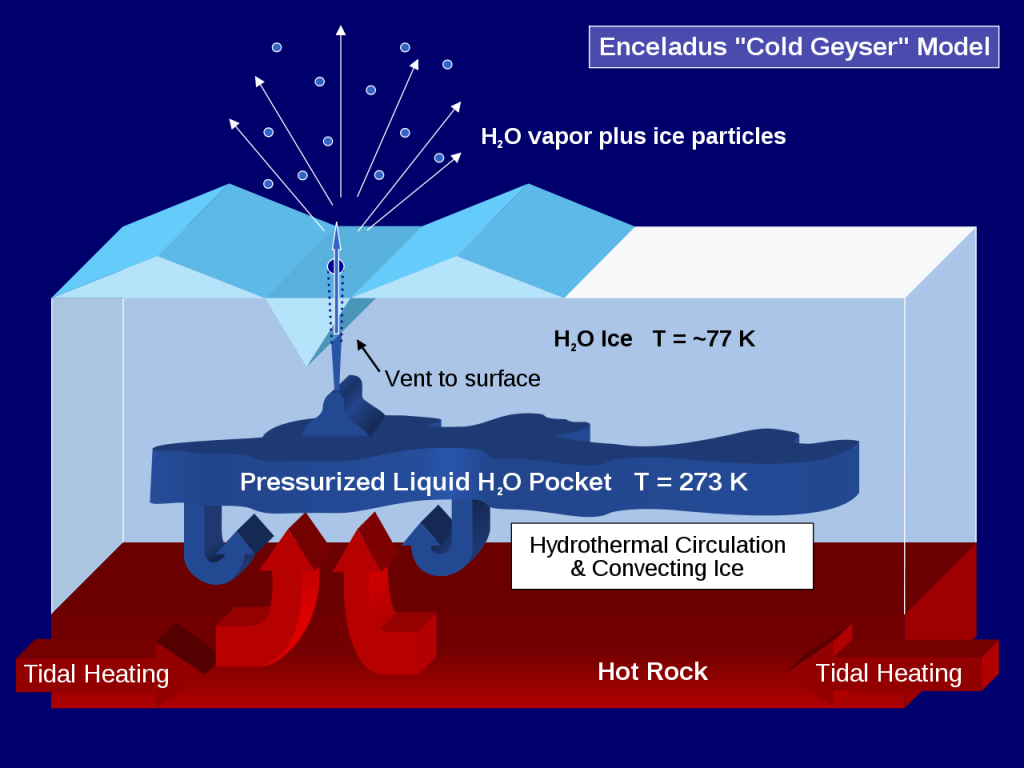
There are indications that Europa also has this kind of geyser activity, although less intense Here is a recent (2021) NASA report, Are Water Plumes Spraying from Europa?

In the search for extraterrestrial life these two moons have top priority. Many proposals for missions to Europa have been formulated and later discarded, here is a list. At the moment the Europa Clipper is being prepared for a launch in October 2024. It will arrive at Jupiter in April 2030. Here is an artist’s concept, of Clipper, Europa and Jupiter. The solar panels of Clipper span 30 meter!

The artist impression might suggest that the Clipper will orbit Europa, but that is not the case, it will orbit Jupiter in an elliptical orbit and make 44 flybys of Europa. It will study Europa’s icy crust, find confirmation for the ocean underneath and try to make flybys through the geysers (if they exist).

A proposed follow-up mission is the Europa Lander. It would land on Europa, collect some material from the icy crust and search for biomarkers, signs of life. Here is another artist impression. Notice the geyser at the horizon 😉 .

Probably the Europa Lander mission will be cancelled. Why? Because Enceladus offers better options than Europa. The main difference is that Enceladus is continuously spewing water and ice crystals, whereas the geysers of Europa are sporadic and still have to be confirmed.

The reason that there is so much interest in the geysers is obvious. To find out if there is life in these oceans, we have to drill through a 15-25 km thick ice crust first. Actually there are studies how to do that, they read like science fiction. Here is the final report (pdf file, 70 pages, 2019) about the Europa Tunnelbot. The basic idea is that this tunnelbot would melt itself down through the ice crust of 20 km in 3 years time, to reach the ocean. Here is a artist impression from the report, I have rotated it 90 degrees, to fit better in this post. Left is the icy surface of Europa, the inset shows three “repeaters” because even when the bot reaches the ocean it still must transmit date to the lander.

Science fiction and I think it will never happen, because the geysers on Enceladus and possibly on Europa may already give information about life in the oceans below the crust!

After Cassini observed the geysers on Enceladus, the scientific program was adapted and the spacecraft went a few times through the plumes. It found water, ice crystals and organic compounds!

So that will be the program for the next decades, explore Enceladus and find out whether the geysers will have convincing biomarkers.. .

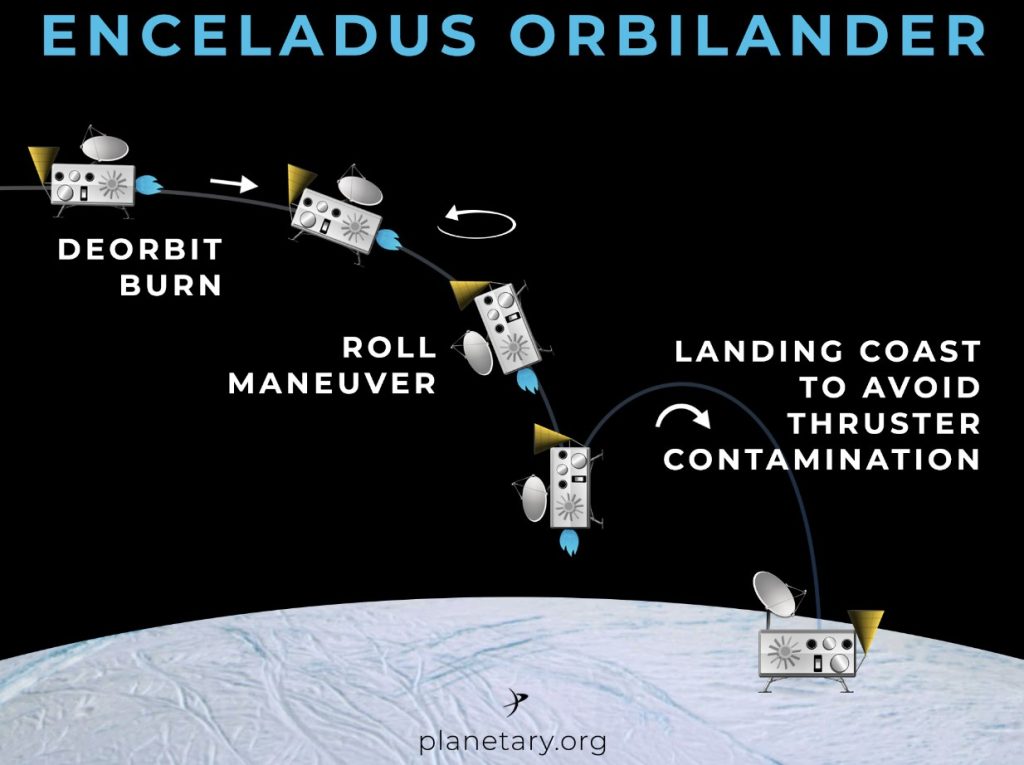
Of course it will take time to design Enceladus missions. Here is one, the Enceladus Orbilander. Approved as a so-called Flagship Mission. Still in the design phase. possible launch in the late 2030s Arriving at Enceladus in the early 2050s.

First it will fly numerous times through the geysers, collect material and analyse it. Then it will land at the South polar region.

This is the South polar region of Enceladus. The “tiger stripes” are fissures in the ice crust where geysers erupt.

And here is an artist impression of the Orbilander on the surface of Enceladus.

Until now life has only be found on Earth. Discovery of (primitive) life elsewhere in our solar system would be dramatic, because in that case we would know that (intelligent) life is ubiquitous in the universe.

At the moment Perseverance is collecting soil samples on Mars which will be brought back to Earth by the Mars Sample Return Mission around 2033. At about the same time Clipper will explore Europa. So we will have to wait for 10 years and for results from Enceladus about 30 years.

Perseverance perseveres

Posted on by
2

On 18 February 2021 the Perseverance rover landed successfuly in the Jezero crater on planet Mars. A few weeks later I wrote a detailed blog about the landing and the mission of the Perseverance: to determine whether Mars ever was, or is, habitable to microbial life. We are now more than two years later, time to give an update. I assume that you have read the first post ;-).

First about the Ingenuity helicopter. There has been a lot of opposition to include the helicopter in the project, many people were worried that it might compromise the main goal of Perseverance. Here are two pictures taken by the WATSON camera (mounted on the robotic arm). Left the Ingenuity still under Perseverance’s belly with its legs unfolded, right next the the rover, ready to fly. Photos taken 1 and 7 April 2021, respectively

Here is a selfie of Perseverance, taken on 6 April 2021 again by the WATSON camera. Notice how small the helicopter is. Do you wonder why you don’t see the robotic arm in this picture? Actually WATSON took 62 pictures, resulting in this composite image, click here for details.

Originally only 5 flights of Ingenuity were planned, just to test if the helicopter could fly in the very thin Martian atmosphere. Because contact with Earth takes about 11 minutes, those flights have to be autonomous. They were so successful that the Ingenuity is still operating now, on 23 April it had its 51th flight. It is actually scouting for Perseverance to find suitable locations to explore. Click here for a list of all flights, full of interesting details. During flight 51 Ingenuity took a picture of Perseverance (upper left corner). Not easy to spot, the right picture shows an enlargement

In my Perseverance blog, I could only be rather vague about details of the mission. The rover was supposed to collect samples of Martian rocks and soil (regolith), using the drill on its robotic arm. Then put these samples in sample tubes and store them in a container. Here is an example of a sample tube, the container can hold 43 of them.

Here is the proposed route at the time when I wrote my blog.. The x marks the landing of Perseverance in the Jezero crater, which was a lake, billions of year ago. In those days a river was flowing into the lake (from the left), creating a delta of sediment. If ever life developed on Mars, this region might be suitable to find proof of it.

And here you see the actual route of the rover during the last two years. It is a screenshot from the NASA website Where is Perseverance? Really worthwhile to visit the site, you can zoom in on the map which is updated regularly. The red markers give the locations where samples have been collected. The blue markers show where the Perseverance and the Ingenuity are.

When you visit the website and zoom in, you will get this. Clicking on a white circle will tell you when the rover was there, clicking on a line segment gives the distance, clicking on a red marker will tell you the number of the sample collected

During the two years that Perseverance has been exploring, it has collected 19 samples, here is the list, with lots of details for each sample.

The first sample was actually a failure, it must have been a shock for the team! Here is a screenshot. Sample Type: Atmosopheric. The core must have been too powdery/brittle, broken into pieces, and the capsule is empty. More about it here .

Fortunately all other sampling attempts until now were successful. Here is an example. The rocky outcrop has been named Wildcat Ridge. Two samples (no 12 &13 in the list) have been drilled and a circular patch of the rock has been abraded to investigate the rock’s composition.

Why two samples from the same location? When you look at the list, you will find that this is the usual procedure. All samples have been collected twice from each location (except the first, failed, one).

In the period between 21 December 2022 and 28 January 2023, one sample of each location has been dropped in what has been called a depot, named Three Forks. I have indicated the location with a red oval in the detailed map above. Here is a picture of the second sample being dropped.

And here is a collage of all 10 samples dropped. THe Atmospheric sample, 8 samples with rock or regolith and one witness sample. A witness tube will follow the same procedure, but not collect any rock or regolith. Back on earth it will be inspected to check for any contamination with material from Earth. Click here for more details.

,The sample tubes tubes are not dropped at the same spot, but about 5-15 meter apart. The center of each circle is the location where that sample was deployed, with in red the name given to the sample (see the list).

Why all this? Basically for safety reasons. The ultimate goal of the mission is to bring the sample capsules back to earth, where they can be studied in much more detail than is possible by Perseverance. In my first blog I wrote that this so-called Mars Sample Return porject at first sight looks like science fiction. And I still think it does 😉 . Here is an outline of the project in its present form.

  • In 2027 the Earth Return Orbiter (ERO) will be launched and reach Mars in 2029 where it will go in orbit and wait for the container with the samples.
  • In 2028 the Sample Retrieval Lander (SRL) will be launched. It will land on Mars in 2029, probably close to the Three Forks depot. It will bring two helicopters and the Mars Ascent Vehicle (MAV), a rocket.
  • If Perseverance is still working properly, it will also travel back to the Three Forks depot. In that case it can transfer its samples to the MAV
  • If not, the two helicopters will transfer the ten dropped samples to the MAV
  • After the samples have been stored in the MAV, it will leave Mars, go in orbit around the planet and release the container with the samples.
  • The ERO will pick up the container with the samples and place them in the Earth Entry Vehicle (EEV). Then it will leave its orbit and travel back to Earth
  • Near Earth the ERO will release the EEV which will “fall” back to Earth. No navigation, no parachute. It is scheduled to land in 2033 in the desert sand of the Utah Test and Training Range.

In this artist impression the Sample Retrieval Lander is at the right, left the Perseverance. The Mars Ascent Vehicle has just been launched, it will bring the container with the precious samples to the Earth Return Orbiter. One of the Sample Recovery Helicopters is hovering in the thin Martian atmosphere.

In the original design, the Sample Retrieval Lander carried another rover which transported the sample tubes from Perseverance to Mars Ascent Vehicle. . It has been skipped because of the success of the Ingenuity helicopter. The Sample Recovery Helicopter has basically the same design, but is stronger, can carry a small load and has wheels. Here is an artist imprssion. It can transport a dropped sample tube, one at a time, from the depot to the Lander.

.Another design change is that the Sample Retrieval Lander has a powerful robotic arm to put the samples in the sample container. Have a look at this fascinating video. The robotic arm picks up a sample tube from the ground, and puts it inside the rocket. But it can do the same with samples stored inside the Perseverance.

Have a look at this animation. You see the Sample Retrieval Lander land near the Perseverance. The robotic arm transfers the sample capsules to the Mars Ascent Vehicle, which is then launched. When in orbit it releases the container with the samples. This container is then collected by the Earth Return Orbiter. There the container will be placed in the Earth Entry Vehicle. All this will take place after the landing of the Sample Retriever Lander in 2029.

At the moment the whole whole retrieval mission is still in the design phase. Here are prototypes of the sample container and the Earth Entry Vehicle. To give you an impression of the size, a sample tube is about 15 cm long. The container is roughly the sise of a basketball. The diameter of the EEV will be about 1.5 meter.

The retrieval operation will take place in 2029, six years from now. The Perseverance is working beyond expectation, but will it still work properly in 2029? In the first phase of the exploration Perseverance has collected dupilcate samples and dropped one of each at the Three Forks depot. In one of the NASA reports I read that in the second phase the Perseverance will no longer collect duplicates.

So, when everything goes well, in 2029 Pereverance will return to the Three Forks Depot with in its belly around 30 collected samples. In that case The Robotic Arm will transfer the samples to the sample container. It will leave the depot untouched! Why? Because the retrieval will be a risky process. The container after launch will be floating in orbit and hopefully collected by the Earth Retrun Orbiter. And near earth the container, now inside the EEV, will be dropped near Earth and hopefully fall down in the Utah desert. I still think it’s science fiction 😉 So, in case something goes wrong, at least there are still 10 samples in the depot, waiting for another mission.

The paragraph above is my own interpretation.

And this is my personal comment, before I finish this blog.

The whole mission until now has been presented as a huge success. And techologically speaking, I agree. But still I think the scientists will be a bit disappointed, because a “smoking gun” has not been found until now.

When (microbial) life developed on earth, 3.5 billion year ago, it left fossil traces behind, called stromatolites, like this one, found in Australia..

Stromatolithe – MNHT

If this kind of sediment would be found in the Jezero crater om Mars, it would be frontpage news all over the world: Life has existed on Mars.

In 2019 a team of NASA/ESA scientists went to Australia to study the stromatolites. In the video they call them the Holy Grail.

But until now no sign. The collected samples contain organic molecules, but that is nothing new, Curioisity, the predecessor of Perseverance already found them.

Of course Perseverance will persevere exploring the sediments in the Jezero delta and collect more samples. Hopefully it will one day be able to take pictures of stromatolite. If not then we will have to wait until 2033 when the samples are returned to Earth and can be investigated in specialised laboratories.

Yes, I think the scientists are a bit disappointed.

The Pillars of Creation

Posted on by
1

In 1995 NASA published this picture, taken by the Hubble Space Telescope. It shows a small part of the Eagle Nebula and became instantly famous. Because in the “pillars” stars are born, the picture got the name “Pillars of Creation”.

The Hubble Space Telescope was launched in 1990 and is still operating, with quite a few Space Shuttle service missions. To celebrate its 25th anniversary, a new picture of the Pillars of Creation was published in 2015. With a new camera installed, more details are visible,

At the same time this picture was published, an infrared picture of the Pillars. Infrared light can travel more easily through dust and clouds and that is why now you see stars in the pillars, where young stars are still being formed. But I hope you wonder how this can be an infrared picture as infrared light is invisible light. The explanation will be the main part of this post.

But first here are two pictures, recently taken by the James Webb Space Telescope. The JWST is an infrared telescope has and has two cameras on board to take pictures. The NIRCAM for near infrared light and the MIRI for medium infrared light. Here is the NIRCAM photo

And here is the image from MIRI, Amazingly different. And again, how can these be infrared pictures’?

f

Time to give some explanation about the pictures and also about the Eagle Nebula, where the Pillars of Creation are located.

———————————————–
About visible and invisible light

Light is an electromagnetic wave, as are microwaves, radio waves, X-rays etc, They all have different wavelengths. The wavelengths of visible light are often given in nanometers (nm), where 1 nm is 1/billionth meter. Or in micrometer (μm) where 1 μm = 1000 nm. The human eye is sensitive to wavelengths between ~380 and ~750 nanometer and sees the various wavelengths as different colors! The longest wavelengths are seen as red, the shortest as purple/blue with all the “rainbow” colors in between.. In this diagram the electromagnetic spectrum is shown. The infrared part can be subdivided in near infrared, mid infrared and far infrared

The Hubble telescope has two cameras onboard. Most of the iconic Hubble pictures have been taken by the Wide Field Camera. The present wide field camera (WFC3) can take photos in two channels, one for ultraviolet and visible light (UVIS) and the other one for near infrared (NIR), The range of UVIS is 200-1000 nm and of the NIR 800-1700 nm

The James Webb has two cameras, the NIRCAM for the near Infrared, range 600-5000 nm and the MIRI for the mid Iinfrared, range 5000-28000 nm (5 μm -28 μm).

Before we describe in some detail how digital cameras record images, it is useful to have a look at the way the human eye sees colors.

———————————————–
How does the human eye see colors?

The retina of the human eye contains about 6 million nerve cells, called cones. These cones come in three different types, S, M and L, sensitive to various parts of the spectrum. The S type cones are sensitive to the blue part of the spectrum and are also often called Blue cones, In the same way the other two are often called Green and Red.

The brain is able to combine the response of these RGB- cells. For some people the M and/or L cone cells are not working properly. As a result they are colorblind.

———————————————–
How does a digital camera record colors?

Digital cameras have sensors consisting of millions of individual pixels that record the intensity of the incoming light, basically in a gray scale (black and white). That these cameras can take color pictures is because in front of the sensor there is a color filter, consisting of a mosaic of millions of red, green and blue “pixels”. A so-called Bayer filter. See the diagram below. Taking a picture, means actually taking a red, green and blue picture at the same time, but these pictures are “incomplete”. By mathematical techniques (interpolation) the full color pictures are constructed.

.

Here is an example, where three images, in red, green and blue, when combined, give the full image in natural colors.

The sensors in space telescopes do not have these Bayer filters, they just record the image in gray scales. However, various filters can be placed in front of the sensor and multiple images can be taken of the same object. For example, the Hubble WFC3 camera has a huge choice of filters, 47 for the UVIS channel and 14 for the IR channel.

Why so many? Some filters are broadband, they pass a wide range of wavelengths. From a scientific point of vew the narrowband filters are interesting because they pass only the light emitted by specific elements. Here is one example, hydrogen (H) emits red light with a very specific wavelength of 656 nm. So one of the filters only passes wavelengths around that value and a picture taken with this filter shows the presence of hydrogen. Similar filters can be used to check the presence of oxygen (O), sulphur (S) etc.

———————————————–
The Pillars of Creation pictures are “false-color” pictures!

On 1 April 1995, astrophysicists Jeff Hester and Paul Scowen published an article The Eagle Nebula, in which they showed a picture of the Pillars of Creation. If you think that was “just” a picture taken by the Hubble telescope, you are seriously mistaken. The PBS/NOVA website More than just a pretty picture explains in 19(!) webpages how the iconic photo was created. Very readable,

The WFC2 consisted actually of four cameras, each recording a quadrant. The top-right quadrant camera was slightly different, zooming to show more details. Resizing it to the format of the other three, causes the characteristic Hubble image with the “steps” in one corner. Here is the original image of this top right quadrant, in gray scales. What a mess. For an explanation how to clean this image, see the website. The second image shows the result of the various cleaning operations. What a difference !

We can do the same for the other quadrants.

top left
bottom left
bottom right

Now we can “glue” the four parts together. You can still see a bit the seams between the four images.

For this mage a filter was used that only let blue-green light through from (doubly ionised) Oxygen atoms (OIII). Two more filters were used to create images in the same way. One filter let only the reddish light from Hydrogen atoms through (Ha), the other one selected reddish(!) light from ionised Sulphur atoms SII). Three narrowband filters, two of them in the same color range.

Here are the three filtered images

SII filter
Ha filter
OIII filter

You might expect that the next step would be to give these image’s color corresponding to the filter used for each of them. The Ha and SII reddish and the OIII one greenish. But that is NOT what Hester and Scowen did. They assigned the RGB colors to the three images. Blue to the OIII image, Green tot the Ha image and Red to the SII image.

SII
Ha
OIII

Final step is to combine them: the Pillars of Creation.

The main reason to assign “false colors” to the pictures is to enhance the contrast and to see how the various elements are distributed. Almost all Hubble photos are false color (also called pseudo color). Using the three narrowband filters for S, H and O and assigning them to RGB is so common that it is often called the Hubble Palette. Doing a Google image search for Hubble Palette gives a huge number of hits. Here is a part.

Other combinations of narrowband filters are also used. Here is an example where 6 filters have been used for the Butterfly Nebula. Besides SII, Ha and OIII, also ionised nitrogen, helium and oxygen. In the table the natural colors are given and also the colors assigned in the Hubble palette.

An American astrophotographer got curious how this nebula would look in the natural colors. Here are two images’, left the false color one and right the picture in natural colors. It is clear that the artificial image reveals many more details

It must be clear now that while with the Hubble telescope you have a choice to use false colors, with the JWST there is no other option, as infrared light is not visible. Here are the filters used for the MIRI camera. The colors suggested for the various infrared ranges are not significant, just to guide the eye.

For the MIRI picture three filters were used, F770W, F1130W and F1500W. In the above diagram I have marked them. For this picture they are assigned Blue, Green and Red respectively.

 

The NIRCam camera has many more filters, broadband, narrowband etc.

For the NIRCam picture 6 filters have been used, marked in the diagram above.

t

I have read somewhere that creating these images should be considered as art and I agree.

———————————————–
The Eagle Nebula

Finally a few remarks about the Eagle Nebula. When massive stars die, they can “explode” as a supernova, erupting their remnants into space. In these clouds of dust and various elements, new stars can be formed. The Eagle Nebula is such a cloud, here is a picture taken by an astrophotographer, using a telescope and a DSLR camera! Many of the bright spots in this picture are young stars already formed in the cloud. These stars are so hot that they emit UV light and even X-rays. This radiation can has enough energy to ionize the cloud. Such a cloud is called an emission nebula. The dominant reddish color is caused by hydrogen

The Eagle nebula is located about 7000 lightyear away and is huge, roughly 70 x 55 lightyear. It is a young nebula, estimated age is 5.5 million year. It is also a temporary event, the forming of new stars still continues and the radiation those stars will erode the nebula.

In the center of the above image, you can see the pillars of creation.Here is a dteail. Comapre it with the images of Hubble and Webb. Even these pillars are huge, the logext one is about 4 lightyear long.

A final remark. From the Hubble and Webb picture you might think that the pillars are almost like rock, impenetrable. But this is not true at all. The density of nebulas varies between 100 – 1 million particles per cubic cm. A high vacuum on earth still has considerably more particles per cubic cm. It is just the huge size that makes the pillars look like solid.

Lagrange points

Posted on by
Reply

On 25 December 2021, the James Webb Space Telescope (JWST) was successfully launched. It has now reached its destination at the L2 Lagrange point of the Sun-Earth system. For many years I have considered writing a blog about the five L:agrange points, but I was not sure if I could do that in a relatively simple way.

I am still not sure, but in this blog I will give it a try.

Here is a diagram of the Sun-Earth system (not to scale). The five Lagrange points are marked.

Earth and all other planets orbit the Sun because of the gravitational attraction between a planet and the Sun. Earth orbits the Sun in ~365 days at a distance of 150 million km. The other planets do the same, but at different distances and with different periods. Here is the solar system (not to scale).

It was Kepler who studied the planetary motion. He found a relation between the period and the distance, which is now called Kepler’s Third Law: The square of a planetary period is proportional to the third power of its distance. Let’s take Mars as an example. The distance to the Sun is ~228 million km and a Mars year is ~687 days. The distance is a factor 228/150 = 1.52 larger. The third power of 1.52 is 1.52×1.52×1.52 = 3.512. Kepler’s 3rd law predicts that a Mars year will be √ 3,512 = 1.88 times longer than an Earth year. = 1,88 x 365 = 686 days.

Now let us consider a spacecraft in the Sun-Earth system. It’s mass is so small compared to the mass of Sun and Earth, that it will not influence their motion. But it will feel the gravitational attraction from the Sun and also from the Earth. Is it possible that the combined attraction of Sun and Earth will result in a period of 1 year?

The answer is yes, there are exactly 5 points where this is the case, the 5 Lagrange points!

Here is the explanation for L2. This point lies farther away from the Sun than Earth, so the attraction from the Sun is weaker and would result in a longer period. But Earth also attracts the spacecraft in the same direction as the Sun and in L2 they give together enough attraction to let this point orbit in 1 year. Calculation gives that L2 is located 1.5 million km from Earth, 151.5 million km from the Sun

For L1 the explanation is similar. Here the attraction of the Sun is stronger resulting in a shorter period. But now Earth “pulls back” and together they give the right amount of attraction. The location of L1 is also 1.5 million km from Earth, 148.5 million km from the Sun (the figure above is not to scale).

L3 lies at the opposite side of the Sun, Here the attraction from Earth is minimal, it contributes only little to the attraction of the Sun, so L3 lies only slightly further away than 150 million km from the Sun.

Before we describe the points L4 and L5, we will first look in a bit more detail at the solar system. When we say that the planets orbit the Sun, it suggests that the Sun doesn’t move itself, while the planets orbit around it. And that is not true. The Sun and a planet both orbit around their common center of mass, often called their barycenter. In this image the barycenter is shown for the Sun and Jupiter. Because the Sun is much more massive than Jupiter, their barycenter lies close to the Sun.

Here are a few animations for different situations, where the barycenter is marked with a red cross. The animations are not to scale. The first image shows the situation of for example two stars of equal mass. The next one shows minor planet Pluto and its large moon Charon. The last image shows Earth and Sun. The mass of Earth is so small that the barycenter lies within the Sun.

Of course the resulting force in the Lagrange points has to be directed to the barycenter and for L1, L2 and L3 this is automatically the case, because these points lie all three on the line connecting Sun and Earth. These points were already found by the famous mathematician Euler in 1720.

In 1772 Lagrange discovered two more “stable” points, where the attraction of Sun and Earth are not in the same direction, but together point to the barycenter. of the Sun-Earth system. .

The mathematics is complicated, I will use some hand waving to make the existence of L4 (and L5) plausible. In the diagram below, the masses of Sun and Earth are S and E , the barycenter is indicated as b, it lies within the Sun because the Sun is much more massive than the Earth. The location of b depends on the ratio of the two masses S and E;.

L4 is the top of a triangle with all sides equal to the distance between Earth and Sun. Because L4 has an equal distance to Earth and Sun, the gravitational forces on L4 are in the same ratio of S and E. Therefore the resulting force is directed to b ! Note that L4 lies outside Earth’s orbit. Similar to L1, the two combined forces give L4 a period of 1 year, same as Earth.

Actually the barycenter of the Sun-Earth system lies extremely close to the Sun’s center of mass, The radius of the Sun is 670.000km and b lies about 450 km from its center! In this diagram this distance has been strongly exaggerated to show the process. In the usual diagrams of the Lagrange points, L4 and L5 are located so close to the Earth orbit, that it is not possible to see their separation.

Until now we have described the 5 Lagrange points as points that orbit the Sun in one year, same as the Earth. Another description is often used, a rotating coordinate system. In such a coordinate system, centered in the barycenter and rotating once a year, Sun, Earth and the 5 Lagrange points are stationary. But it comes at a cost. Because such a coordinate system is not an inertial system, fictitious forces have to be introduced, for example the centrifugal force,

In the diagram below the Lagrange points are indicated, in such a rotating frame. The contour lines give the gravitational field energy. Compare it with the contour lines on a topo map. The blue and red arrows indicate the direction of the force (the direction of the slope in a topo map). In topo map terminology L4 and L5 are located on the top a hill, while the other three are located in so-called saddle points. On first sight it would seem that all Lagrange points are unstable, For the L1-L3 points a small displacement in the x-direction, and for L4 and L5 a small displacement in any direction would be enough to disturb the balance (like a pencil on its tip).

Careful and complicated mathematical analysis (see for example here) leads to a surprising result: the regions around L4 and L5 are actually stable, objects in a large region around these Lagrange points will move in orbits and stay in that region. The regions around the other three Lagrange points are unstable, objects can orbit for a while, but will eventually escape. That is illustrated in the two diagrams below. The left diagram. shows the Sun-Earth system in an inertial frame, the right one in a rotating frame The 5 Lagrange points are marked in red.

Notice the moving tiny points, They are test masses. released near the various Lagrange punts. Look carefully and you will see that the test masses released near L1 and L2 quickly move away. For L3 it takes a bit longer. All these three Lagrange points are unstable. But around L4 and L5 the test masses do not “escape”, these points are stable.

In the introduction of this blog I wrote that the JWST had reached its destination at the L2 Lagrange point of the Sun-Earth system. Actually the space telescope is not positioned in :the Lagrange point itself but orbiting L2. And what an orbit it is! Elliptical, the distance to L2 varies between 250.000 km and 832.000 km. One period takes about 6 months. The orbit is not stable, about every 21 days the thrusters of the JWST must perform minor course corrections.

A more detailed explanation of the WEBB launch and orbit can be found in this brilliant YouTube video: How James Webb Orbits “Nothing”

There also satellites orbiting L1. At the moment for example the SOHO satellite to study the Sun and the DSOVR to study the Earth. Here are two pictures taken by these two spacecraft.

In 1978 the International Sun-Earth Explorer-3 (ISEE-3). was the first spacecraft that went into an orbit around a Lagrange point. It studied the Sun and Earth for 4 years and also here the unstable orbit had to be corrected regularly. Here is a diagram of the launch process.

After its mission was completed, the spacecraft got a new target, to study comets! It was renamed International Cometary Explorer, left its orbit and via amazingly complicated manoeuvres went on its way to a comet., Click on the screenshot to see an animation of the mission. Very informative and fascinating..

What about L3? This Lagrange point is permanently behind the Sun, as seen from the Earth. No scientific use, but it has played a role in science fiction. . Here is an example, a science fiction movie Journey to the Far Side of the Sun, released in 1969 (the same year that humans landed on the Moon). Click on the screenshot to watch the movie.

Synopsis of the movie: In 2069 a planet is discovered in L3 and the director of Eurosec (named Jason Webb !) organises a mission to what turns out to be a mirror-earth. Very interesting to watch.

We now know that L3 is unstable, with a “decay time” of about 150 year. It would be a suitable location for alien enemies to hide, while preparing for an attack 😉

L4 and L5 are stable (under certain conditions) but have no use for science. Possibly in the far future, these regions could be used to build human colonies.

Until here we have concentrated on the Lagrange points of the Sun-Earth system, but the Earth-Moon system has also its Lagrange points and so do for example the Sun and Jupiter.

Jupiter has collected thousands of asteroids around its L4 and L5 points. They are called trojans because they are named after heros of the Trojan war. Here is an animation. The asteroids in front of Jupiter are called the Greeks and the ones trailing Jupiter are called the Trojans.

The name trojan is now generally used for objects in the L4 and L5 points of other planets. In the L4 and L5 points of the Earth until now “only” two Earth trojans. have been observed.

But there may have been one in the early history of Earth!. I will end this blog with a fascinating theory about the origin of the Moon! The theory is called the Giant-Impact Hypothesis. When the Sun and the planets were born, about 4.5 billion year ago, Earth was not alone. It had a Mars-sized sister planet in the L4 (or L5) Lagrange point. About 20-30 million year later, this hypothetical planet, named Theia, possibly disturbed by the other planets, left the L4 region and collided with Earth. It must have been a cataclysmic event From this collision the Moon was born.. Here is the scenario.

And a visualisation

Here is the Wikipedia List of Objects at Lagrange Points

All the images are taken from the Internet, many from Wikipedia.

The DART mission

Posted on by
2

Two years ago I published a detailed blog post: Will an asteroid hit Earth? In that post I discussed the scenario that an asteroid had been discovered on a collision course with Earth and what could be done to avoid such a possibly catastrophic collision. One option is to send a spacecraft to the asteroid and let it crash with it. The impact should change the course of the asteroid, so it would no longer hit Earth.. The DART mission will test the feasibility of this “kinetic impactor” technique. DART will be launched on 24 November, so it is time for an update.

The acronym DART stands for Double Asteroid Redirection Test. Target for DART is the minor asteroid Didymos, discovered in 1996. It has a diameter of 780 meter and orbits the sun in 2.11 year. In 2003 it was discovered that Didymos has a small moon with a diameter of 160 meter. This moon has been named Dimorphos , it orbits Didymos in about 12 hour at a distance of 1.2 km. DART will crash into this moon at a speed of 6.6 km/s. and change its orbit slightly. In the infographic this change is hugely exaggerated. It is estimated that the crash will change the speed of Dimorphos only about 0,4 mm/s and its orbital period about 10 minutes

Originally DART was part of the much more ambitious AIDA mission. The crash will take place at about 11 million km from Earth. How to observe the effects of the crash? The solution was to launch another spacecraft earlier than DART, which would reach Didymus and go into orbit around the asteroid. This AIM spacecraft , to be developed by the European Space Agency (ESA), would observe the crash and send data back to Earth. It would even deploy a small lander, MASCOT2 to study the properties of Dimorphos.

But in December 2016, AIM was cancelled by ESA, after Germany withdrew the 60 million Euro funding for the project. I commented in the above mentioned blog:

As an European I feel rather ashamed that Europe has acted this way.

NASA decided to continue with DART., which will be launched by a SpaceX Falcon 9 rocket. A fascinating feature from the Falcon 9 is that part of it (the first stage) will return to Earth, land vertically (!) and can be used again for other missions. It will land on a so-called drone ship, an unmanned platform in the ocean. There are three of these drone ships active at the moment, all with poetic names. The Falcon 9 will land on “Of Course I Still Love You” Here is the ship.

And here is a video of the take off and landing. You must see it to believe it ;-).

DART will arrive at the asteroid end of September 2022. The spacecraft will use autonomous navigation to point itself to the moon. It has a camera on board, the DRACO that takes high-resolution photos. On-board software will analyse these photos, be able to distinguish between Dimorphos and Didymos and point Dart to Dimorphos.

About 10 days before reaching its destination, DART will deploy a tiny spacecraft, a so-called CubeSat . This LICIACube has been developed by ASI, the Italian Space Agency and will take pictures of the crash. So at least images of the collision will be sent to Earth.

Here is a short YouTube video of the DART mission. I will point out a few details.

  • 0:07 The nose cone of the Falcon 9 opens to deploy DART
  • 0:15 the solar arrays are unrolled, a new technique. Each one is 8,5 m ;long
  • 0:22 The lens cover of DRACO opens
  • 0:26 Didymos in the center, Dimorphos to the right
  • 0:32 The orbits of Earth and Didymos. They comes close, but are still 11 million km away from each other when DART crashes.
  • 0:37 The Xenon thruster will steer the spacecraft
  • 0:41 The LICIACube is deployed
  • 0:54 DRACO will find the target
  • 0:58 Found the target
  • 1:02 On collision course
  • 1:04 The end of DART

My next update about DART will probably be in October next year.

The Witch’s Broom Nebula

Posted on by
Reply

In April the ESA/NASA project published this stunning image as its Picture of the Week. In this blog I will first show some pictures and then give an explanation and some background information.

The image was taken by the Wide Field Camera 3 of the Hubble Space Telescope.

The image shows a very small part of the Witch’s Broom Nebula, also called the Western Veil Nebula. I have marked the (tiny) location of the detailed image with an x (click to enlarge)

This nebula is in its turn part of the Cygnus Loop. Upper right the Witch’s Broom Nebula, lower left the Eastern Veil Nebula.

Getting confused? Here is the relation between the various images. Left the Cygnus Loop, in the middle the Witch’s Broom and right the detail.

The Cygnus Loop is located in the constellation Cygnus (the Swan). Deneb and Vega are very bright stars. The Cygnus Loop (Veil Nebula) is marked in the lower left

This YouTube video may also help

_______________________

About the Cygnus loop and the Veil Nebula

The Cygnus loop and the Veil Nebula are the remnants of a supernova. Many thousands year ago a massive star (much more massive than our Sun) had used up all its “fuel” and exploded in a final spasm before dying. In that explosion, much of the star material is ejected, leaving behind a neutron star or even a black hole. For a short period the star can outshine its whole galaxy!

In this NASA infogram, the development of such a massive star is given. It contains lots of information, but you can skip the details for this blog.

Much research has been done about the Cygnus Loop, the Veil nebula and the star that caused it. The Cygnus Loop is huge, its diameter is about six times the diameter of the moon. You need basically a telescope to see it.

It is a so-called emission nebula. The gas and dust in the nebula is ionised by the shockwave of the exploded star and the light we observe is the light emitted by the atoms in the nebula. The color of the emitted light depends on the kind of element. Very simplified: hydrogen emits reddish light, oxygen bluish light etc. When you look at the image of the Witch’s Broom nebula, you see that it mainly consists of (ionised) hydrogen and oxygen.

Determining the distance of the Cygnus Loop is a complicated process and you will find many values on the Internet. A distance of ~ 2400 lightyear is nowadays accepted by most astronomers. This would give the actual size of the Cygnus Loop as 130 lightyear! The loop is still expanding with a speed of ~ 1.5 million km/h

When did the star explode? Many different estimates. In the release of the first picture above a value of ~10000 year is given ( and a distance of 2100 lightyear). Humans living in that time would have observed the sudden appearance of a very bright “new” star, brighter than Venus and probably even visible in broad daylight. That explains the name (super)nova with nova meaning new in Latin. Supernovae are very rare, the last one in our own Milky Way, visible from Earth, was observed and studied by Kepler in 1604.

Scientists are still searching for a neutron star, or a blackhole in the center of the nebula, but until now nothing has been found.

A lot more can be said about supernovae. In the infogram above they are called “Engines of Creation” and that is an apt description. After the Big Bang the Universe consisted of hydrogen and helium, there was no oxygen no sulfur, no calcium, no iron etc. But Earth and all living creatures are built from those elements. How come? The answer is simple, all those elements have been formed inside stars! We are literally Star Children.

_______________________

About the pictures

The Wide Field Camera of the Hubble Space Telescope takes colorful pictures. Wrong! It takes black and white pictures as do basically all other telescopes. But it uses a filter to select only a specific color (range). And it takes pictures of the same object using other filters, selecting different colors. For the picture above with the stunning details of the Witch’s Broom five filters were used. And those filters are not just simple pieces of red, green or blue glass. A widely used filter is the H-alpha filter, that only lets through the red light of hydrogen (technically: a wavelength of 656 nm, bandwidth a few nm). Here is a picture of the Cygnus loop, using a H-alpha filter.

Compare it with this photo, taken with a color camera without any filters. Dominated by the numerous stars, the Witch’s Broom nebula is (almost) invisible,

Other popular filters in astrophotography are SII and OIII filters They select the colors of ionised Oxygen blueish and Sulfur (reddish) respectively and block all the other colors.

Combining pictures, taken with different filters, you must assign colors to the black and white images. One option is to choose colors that correspond closely to the color of the filter. In that case the result will look more or less “natural”. The red-blue image of the Cygnus loop is a result of combining the H, O and S filters. But of course you can assign different colors to the B&W pictures. Like in the image below, where hydrogen is green(!), oxygen blue and sulfur red.

The Hubble Space Telescope can also use infrared or ultraviolet filters. Here is the Cygnus loop in ultraviolet, blue has been assigned to the B&W image.

The Hubble website has a very informative section The meaning of color in Hubble Images. It shows how the B&W images can be combined in various ways. Very readable, with examples. Here are three.

Left is Mars, where the three filters have been assigned their “real” color. In the middle the famous “Pillars of Creation”, a star forming region. The red hydrogen is depicted in green, the red sulfur light in red and the green oxygen light in blue. The last example shows Saturn in unusual colors, because the B&W pictures were taken with various infrared filters. Near infrared is shown as blue, the middle range as green and the far infrared as red.

Finally here is again April’s Picture of the Week . The text says that It is a combination of five B&W images, Hydrogen in red, oxygen in blue and sulfur in green. No information about the other two.

Dust Grabbers

Posted on by
2

Two years ago I have written a post, Hayabusa2 , about a Japanese spacecraft and a few months later an update, Solar System Explorers, in which I mentioned the American spacecraft Osiris-Rex.

The two spacecraft have in common that they have a similar mission: travel to an asteroid, collect some surface material from it and bring that back to Earth. That’s why I have given this post the frivolous title of Dust Grabbers.

When I wrote the two posts, both spacecraft had arrived at their respective destinations, but had not yet collected asteroid material. Now they have, so it is time for an update.

First about Hayabusa2. Here are asteroid Ryugu and the Hayabusa2 spacecraft.

After reaching Ryugu, Hayabusa2 had already successfully dropped two Minerva rovers and the Mascot lander on the surface of the asteroid (see my first report). The surface of the asteroid was much rougher than expected, here is a picture taken by one of the Minerva’s.

For the touchdown, Hayabusa2 needed a flat surface, without boulders or big rocks and it was difficult to find a suitable location. In my first report I have described the touchdown, here is a very informative animation of the process. Two screenshots, left just before the touchdown, right just after. Notice how flat the asteroid surface is in the animation.

The touchdown was originally planned for October 2018 but postponed, to give the scientists time to redesign the touchdown procedure and check if navigation could be made accurate enough to land in a very small region.

On 6 February JAXA (the Japanese equivalent of NASA) published an extensive pdf-file for the press, Asteroid explorer, Hayabusa2,reporter briefing with a detailed description of the redesigned touchdown. A location had been selected and a target marker (TM) had been dropped near the chosen location. A TM is a small (10 cm) ball of reflecting material, you can see it in the animation screenshots above, left in the foreground.

The actual touchdown finally took place on 22 February 2019. One day earlier Hayabusa2 had already descended slowly from its home position (HP) at 20 km altitude to an altitude of 45 m. Here is a time diagram of the touchdown phase. Notice that between 7:07 and 7:50 JST time, there is no communication between the spacecraft and mission control.

Also keep in mind that the touchdown is an autonomous process, because it takes 15 minutes for a signal from Earth to reach the spacecraft. All steps have been programmed by the scientists and engineers.

Try to imagine the tension in Mission Control during this “blackout” period. And the explosion of joy when the first signals from the spacecraft showed that it was still alive.

At first this is the only thing they know, that Hayabusa2 is still alive. Only later images and data were coming in. A small video camera was mounted next to the collecting horn and recorded the touchdown. Have a look at the video Here are two screenshots, before and after touchdown. I have indicated the position of the target marker, it is the white stip inside the blue circles. Also notice the surprising amount of rubble whirled up after the touchdown, mostly caused by the thrusters firing.

Originally a second touchdown was planned at a different location, but this was cancelled because of the rugged surface of Ryugu. Instead the scientists concentrated on the most ambitious part of the program. The first touchdown had collected some surface material of the asteroid. Technically called regolith . This material has the same age as the asteroid itself, but has been exposed during millions of years to solar wind and radiation.

Of course it would be very interesting to collect some asteroid material from BELOW the surface. Here is the ingenuous plan developed by the Japanese scientists:

  • shoot a projectile to Ryugu to create an artificial crater.
  • touchdown later in the crater to collect some newly exposed material.

And that’s what they did! I have described the working of the so-called SCI (Small Carry-on Impactor) in my first post. Basically it is a copper projectile (2 kg) that hits the surface of Ryugu with a speed of 2 km/s, creating a crater of several meters diameter. Here is a diagram of the operation. Lots of details, I will point out a few. The operation took place on 5 April 2019.

Hayabusa2 descends from HP to an altitude of 500 m and releases the SCI with a downward speed of 20 cm/s. Here you see a time-lapse of the deployment. It takes about 40 minutes for the SCI to reach the surface and detonate. The detonation will cause a lot of debris, so Hayabusa2 must take shelter and does that by moving horizontally away and then down into the “shadow” of Ryugu.

Before disappearing below Ryugu’s horizon Hayabusa2 deployed a camera (DCAM3) to take pictures of the explosion. Here are some images. Not that spectacular for a layman, but apparently the scientists were able to draw conclusions from the vague plumes of debris that are visible.

Because of Ryugu’s weak gravitation it takes days before the debris of the explosion settles down. Notice times and distances in the diagram, Hayabusa2 moves away horizontally for about 100 km before “climbing up” again and finally reaches HP more than 10(!) days after the deployment of the SCI.

After the successful creation of an artifical crater, Hayabusa2 descended a few times above the crater to explore the new situation. Was it feasible to touchdown in or near the crater to collect material, exposed by the explosion, without jeopardizing the success of the first touchdown? On 8 July Jaxa published a very readable report discussing the pros and cons of a second touchdown: To go or not to go . It was decided to go and have a touchdown in the region C01-Cb, not really inside the crater but on the rim. Here are two images to show the touchdown area. The left image shows the artifical crater at the bottom right, the right image gives details about the size of rocks near the touchdown.

The procedure for the second touchdown was basically the same as for the first one. During one of the descends a target marker was released and on 11 July 2019 the touchdown took place. A sample was collected successfully.

Mission accomplished, time to go home. How to deliver the two samples to Earth? Have another look at the Hayabuss2. I have indicated the Sampler Horn and the SRC, the Sample Return Capsule. In this tiny (40 cm diameter) capsule the two samples have been stored (right diagram) and it is this capsule that will be released when Hayabusa2 arrives back at Earth.

After leaving Ryugu on 13 November 2019,Hayabusa2 l will reach Earth on 6 December 2020, using its ion engines for navigation.

Here is a diagram of the SRC return. The capsule will enter the Earth atmosphere with a speed of 12 km/s, the heat shields will protect the sample container. At 10 km altitude a parachute will be deployed.

The planned landing location is the Woomera desert in Australia, about 450 km north-west of Adelaide. Expected landing 6 December between 2:47-2:57 JST. It will take time to find the capsule, hopefully within one day. Here is a photo of the Woomera desert.

JAXA is maintaining a monumental website about Hayabusa2, updated with the latest news: JAXA Hayabusa2 Project.

After this long report about Hayabusa2, I will be much shorter about the Osiris Rex mission. Here is asteroid Bennu, smaller (~500 meter) than Ryugu (~ 900 meter). Both asteroids are spinning fast (~ 4 and ~ 8 hours respectively) and that might partly explain their similar shape of a “spinning top”. Although the material of these asteroids is about 4.5 billion years old, both were probably formed after a catastrophic collision of parent asteroids, millions of years ago.

The Osiris Rex spacecraft has a similar design as the Hayabusa2, with a SRC csapsule for the collected asteroid material. But there is one big difference, instead of a sampler horn, the Osiris Rex has a robotic arm, which can be unfolded and grab regolith while the spacecraft is hovering above the surface.

This has its advantages. The Hayabusa2 has to touch the surface (through its horn) and therefore has to worry about rocks nearby. The robotic arm is longer (about 3 meter) and more flexible. Another advantage is the way of collecting regolith. The Hayabusa2 fires a tiny bullet inside the horn and catches the regolith that is swirling upwards. That will not be much, the team is hoping for 1 gram (!) of material. Only after the capsule is opened the mass of the samples can be measured.

The TAGSAM robotic arm of Osiris Rex works very differently. As soon as the sampler touches the surface, nitrogen gas is blown through the arm and regolith will be collected, almost like a vacuum cleaner. Here is a nice animation of the process.

The TAGSAM procedure took place on 20 October 2020 and was very successful, it is estimated that about 60 gram was collected. (For physicists: how can they know that now already? By using a clever trick, rotating the spacecraft and unfolded robotic arm before and after collection, a difference in the moment of inertia will be observed)

The spacecraft will leave Bennu next year and will return to Earth on 24 September 2023, deploying the SRC capsule to land in the Utah desert.

These has been close cooperation between JAXA and NASA. They will share a percentage of the collected material with each other.

TRIVIA:

Brian May, the lead guitarist of Queen, is also an astrophysicist and quite interested in the Hayabusa2 project. During a Queen tour in Japan in January 2020, he met a few project people: Meeting Brian May.

Because of the Covid19 pandemic, the Japanese Sample Collection Team had to arrive early in Australia (with special permission) and first go into 14 days compulsory quarantine . Here a team member is standing at the heliport where the search for the capsule will start.

Betelgeuse

Posted on by
1

Most of you will know the constellation of Orion. Here is an image taken by the Hubble Space Telescope. The bright reddish star, forming the left shoulder of the Hunter, is called Betelgeuse. Recently this star has been in the news, because there were indications that it might explode in the (near) future.

With the present level of light pollution, it is often difficult to observe the colors of stars, and you will see only the brightest. Of course a star closer to the Sun will look brighter than a star many hundreds of lightyears away. Taking the distance into account, astronomers can determine the intrinsic brightness of a star, called the luminosity. When you plot the luminosity of stars against their color, you get the diagram below. It’s called the Hertzsprung–Russell diagram, named after the two astronomers who created it around 1910.

As you see, the diagram has a lot of structure and it has helped astronomers a lot to understand how stars evolve. The vertical axis gives the luminosity, in units of the Solar luminosity, while the horizontal axis gives the surface temperature of the star, which is directly related to its color. Notice that the temperature decreases from left to right.

The position of some well-known stars is indicated. Of course our Sun, a yellowish star. Betelgeuse can be found in the upper right corner. it has a luminosity of ~ 100.000 times the Sun ! It is a so-called Red Supergiant Star. A giant star, it’s size is about 900 times the size of the Sun. If it would replace the Sun, we would be swallowed, it would extend to the orbit of Jupiter. The reddish color means that its surface temperature is about 3000K

There are also Blue Supergiant Stars. An example is Rigel, also in Orion (his right leg) with a surface temperature of 11000 K. And there exist White Dwarf Stars, with a size 0.1-0.01 times the Sun, and Giant Stars.

Along the diagonal in the HR diagram you will find the Main Sequence Stars. Most stars are located in this band. Here is a plot of 23000 individual stars in the HR diagram

To understand what will happen in the (near) future to Betelgeuse, I must explain a bit about how stars are formed and how they evolve. Stars are born when clouds of interstellar matter (mainly hydrogen and helium) contract as a result of their own gravity. This contraction increases the temperature in the interior of the cloud until the core becomes so hot ( about 15 million Kelvin) that fusion of hydrogen becomes possible. The energy and radiation from this fusion stops the gravitational contraction, a star is born! Here is a very simplified picture of the fusion process.

Let’s look at the star nearest to us, our Sun, It was born about 4.6 billion years ago, and its total lifetime is estimated to be around 10 billion year, so at the moment it is about halfway its life. Here is a sketch, the fusion takes place in the core, the radiation is transported to the surface (photosphere), resulting for the Sun in a surface temperature of about 5800 K and an orange color.

For a heavier star than the Sun, the inward pressure due to its gravity is stronger, so the counter pressure of the fusion in the core must also be stronger to create a balance. Here are some of the effects:

  • The star is bigger and brighter
  • Its core temperature is higher, the “burning” of hydrogen faster
  • The surface temperature is higher, the color more blueish/whitish
  • The lifetime of the star will be shorter

Here is an example: Sirius, the brightest star in the sky. Its mass is two times the mass of the Sun. Compared to the Sun, its radius is 1.7 times larger, its luminosity 25 times larger, its surface temperature is almost 10.000 Kelvin and its lifetime is only about 240 million years. Heavier stars will live even shorter.

We can now explain the Main Sequence in the HR diagram. It is the location of all “normal” stars, who are burning hydrogen in their core. At the lower right we find the low-mass stars, sometimes called red dwarfs , who burn their hydrogen so slowly that their lifetime is many hundred billions of years, longer than the current age of the Universe! At the top left, high-mass stars burn their hydrogen so fast, that in spite of their large mass they have lifetimes of only a few million(!) years.

What happens after the hydrogen fuel in the stellar core is exhausted? That depends on the mass of the star. We will concentrate in this post on the high mass stars (more than 8-10 solar masses), because Betelgeuse is one of them.

In these massive stars, after all hydrogen in the core has been fused into helium, gravitation will contract the core further, raising its temperature, until helium starts fusing into carbon. At the same time the outer layers of the star expand dramatically, while cooling. The star enters its (red) supergiant phase.

The triple-alpha process, as it is called, generates less energy than the hydrogen fusion. Three helium nuclei fuse into on carbon nucleus. Another simplified image.

When the core has fused into carbon, the process repeats. Gravitation contracts the core, its temperature increases , and another fusion process starts, leading to a neon core. Next an oxygen core, a silicon core and finally an iron core. Here is a sketch. A few comments. Notice the difference in scale. The outer layers of the red giant extend to the orbit of Jupiter, whereas the core has about the size of Earth! As you see, the central core is surrounded by layers of lower temperature where still fusion of hydrogen helium, etcetera is going on. It’s like the layers of an onion.

The red supergiant phase doesn’t last long, astronomically speaking, the energy of these fusion processes is much less than the hydrogen fusion. Here is an estimate of the time spent in each of the phases for a star of 25 solar masses. Notice the columns for temperature and density.

When the core has become iron , no more energy can be obtained from fusion and the end of the star is near. Gravity will finally win, the core implodes into a neutron star or a black hole while the outer layers are blown away in a cataclysmic explosion. It is called a (Type II) supernova. During a couple of weeks, the supernova may outshine the galaxy it belongs to and release more energy than the Sun during its whole lifetime. If the supernova is not too far away from us, it may become the brightest star in the sky, even visible during daylight. It looks like a new star (nova = new in Latin), but actually we are watching the last throes of a dying star.

Supernovas are extremely rare, they occur about once every 50 years in a galaxy the size of the Milky Way. A few have been recorded in human history, nowadays many more have been observed in other galaxies. In 1054, Chinese astronomers observed a new star, so bright that during a few weeks it was visible during daylight. Their accurate description made it possible for modern astronomers to conclude that it was a supernova (SN1054) and to identify the Crab Nebula as the remnant of this supernova. Here is the Crab Nebula. At its center a neutron star has been found, the Crab Pulsar.

Click here for a list of supernovae that are of historical significance. The most recent one in our own Milky Way galaxy was Kepler’s Star, observed in 1604, more than 400 years ago!

Time to go back to Betelgeuse. As mentioned in the beginning of this post, it is a red supergiant star at a distance of about 640 lightyear from us. Its mass is about 12 solar masses and its estimated lifetime about 8 million year. It has fused all the hydrogen in its core and is now burning helium in its core. Here is a computer animation of how Betelgeuse might look like.

The gigantic (convection) bubbles are characteristics for this kind of stars. Our Sun has them too, but on a much smaller scale.

Betelgeuse is a variable star, it changes its brightness in a rather irregular way. Here is a graph showing the brightness of Betelgeuse between 1990 and now..

From the right part of this graph you may understand why first astronomers and later the media and the general public became so excited about Betelgeuse. Starting October 2019, the star began to fade more than usual, and by the end of January 2020 it had dropped almost a factor 3 in brightness. A very noticeable difference, here are two photos.

Could it be that this dimming was a signal that Betelgeuse was on its way to become a supernova? It would be a spectacular event, the star might become as bright as the moon and be visible in daylight for many weeks. A harmless event too, the distance of 640 lightyear is too far away. By the way, light from Betelgeuse takes 640 year to reach us, so it could have been exploded already, without us knowing it yet 😉 .

Here is an example of a newspaper headline, in this case the Daily Mail , 23 December last year.

Not surprisingly observers from all over the world have been looking at Betelgeuse the last few months, as you can see in the graph below, notice the density of observations in the last three months :-).

I am sure it must have been a disappointment for many that the last month, the fading stopped and Betelgeuse started to become brighter again.

The last few weeks scientific papers are appearing with possible explanations for the unusual dimming. Probably it has been caused by dust. Supergiant stars regularly spew out some of their material into space, where it may condense into grainy particles, temporarily blocking the light of the star.

So, no supernova? Well, on the long term, it will. Betelgeuse is dying and will go supernova. That can happen in our lifetime, but it can also take 100.000 years or even more (see the table above with lifetimes of the various fusing phase).

I will end this post with two short paragraphs about related topics.

  1. This blog is about massive stars. Our Sun, a dwarf star, has not enough mass to become a supernova. After exhausting the hydrogen in its core (in about 5-6 billion year) , it will start fusing helium into carbon and oxygen and become a red giant star, swallowing the inner planets, Earth included. But there the fusion stops. Gravity takes over, and the Sun will end as a white dwarf.
  2. In massive stars, fusion ends when the core has become iron & nickel, because further fusion would need energy instead of releasing it. However, during the supernova explosion so much energy is released that elements heavier than iron can be created. Our Sun is a second-generation star, it was formed from an interstellar cloud that contained, besides hydrogen and helium, already material from earlier supernovae. Earth and everything in it, consists of atoms that have been formed in the interior of stars. We are Star Children, each atom in our body (except hydrogen), has been created inside a star!

Night Watch & Starry Night

Posted on by
Reply

Hundred years ago, in July 1919, the International Astronomical Union was founded and to celebrate this centenary, an interesting event has been organised, called NameExoWorlds.

A list was prepared of 112 exoplanets and each exoplanet was assigned to an IAU member state. The member states had to organise a public competition to find a suitable name for the exoplanet and its host star. The campaign started in June 2019 and on 17 December the chosen names have been published.

The exoplanet assigned to the Netherlands was HAT-P-6b, orbiting the star Hat-P-6 . Hat-P-6 is a star in the constellation Andromeda, at a distance of 910 lightyear, 30% more massive and also hotter than our Sun. The exoplanet Hat-P-6b has been discovered in 2007 through the transiting method.

It is a gas giant, slightly heavier than Jupiter, orbiting in less than 4 days around its host star. It is an example of what are called Hot Jupiters. Not suitable for life. Here is an image how Hat-P-6b might look like. Much larger because it is hot.

In the Netherlands the public came with more than 6000 suggestions. Most popular were the names Nijntje (for the planet) and Moederpluis (for the star). They are Dutch cartoon characters, famous all over the world. Here is a Japanese version.

A problem was that theses names are copyrighted, so finally number 2 on the shortlist was chosen. Night Watch for the planet and Starry Night for the star.

The Night Watch is a world famous painting by Rembrandt (1642).

And Starry Night is another famous painting, by van Gogh (1889). Now in the Museum of Modern Art in New York.

Are you interested about other exoplanets in the list? Click here and type the country name in the search box.

Or maybe you want to know which names other countries have chosen for their planet and star? Click then here .

As Malaysia is my 2nd home, I will show the results for Malaysia. Here are the exoplanet and the host star

HD 20868 is an orange dwarf star in the constellation Fornax, 156 lightyear away from us and 25 % smaller than the Sun. Its planet HD 20868b is also a gas giant, but orbiting farther away from its star in about 1 year. In the habitable zone, but as it is a gas giant, probably not very suitable for life.

I have no info about the campaign, apparently 1635 proposals have been made. Here is the final choice: the planet and star have been named after the Malay names of gemstones , Baiduri (Opal) for the planet and Intan (Diamond) for the star.

It is quite fun to see what other countries have chosen!

Nobel Prize Physics 2019

Posted on by
Reply

The Nobel Prize for Physics has been awarded this year to Jim Peebles for ” theoretical discoveries in physical cosmology” and to Michel Mayor and Didier Queloz for “the discovery of an exoplanet orbiting a solar-type star”.

It happens regularly that the Nobel Prize is split, but in this case there is hardly a connection between the two topics, and the Nobel committee must have realised that,  by adding that the prize this year was won for “contributions to our understanding of the evolution of the universe and Earth’s place in the cosmos”

In this post I will concentrate on Jim Peebles, maybe in a later post I will write more about the discovery of the other two physicists.

The scientific career of Peebles is closely associated with the Cosmic Microwave Background (CMB) radiation, so I will first explain what it is and how it was discovered.

According to the Big Bang theory, the Universe came into being 13.8 billion year ago. Incredibly tiny, hot and dense, it started to expand, while cooling. In the beginning it was a soup of gluons and quarks, but after a few minutes (!) the temperature had dropped so much that “normal” matter, like protons, neutrons and electrons became stable and even some light elements like deuterons and alpha particles could be formed. But it was still a plasma for many thousand years, until after around 380.000 years the universe had cooled so much that electrons and nucleons could form neutral atoms, like helium and hydrogen. From that time onwards until present photons could travel freely, the Universe had become transparent.

In the 1960’s Dicke and Peebles at Princeton studied this Big Bang theory, which was still not universally accepted at that time. If the Universe started with a “primordial fireball” , remaining radiation of this fireball should still be present. But the Universe has expanded about 1000 times since it became transparent, so the wavelength of that radiation has also increased 1000 times! No longer visible (reddish) light, but microwaves with a wavelength in the order of cm/mm’s, corresponding to a temperature of only a few Kelvin.

To detect this kind of radiation you need a microwave radiometer , and two colleagues of Dicke and Peebles, Roll and Wilkinson, also at Princeton, were building one. Then they learnt that two scientists at Bell Laboratories, Penzias and Wilson, only 60 km away from Princeton, were actually working wich such a radiometer and had found results they could not explain. Here is a photo of the Holmdel Horn Antenna, used by Penzias and Wilson.

What was it they could not explain? Well, measuring microwave radiation is not easy, because there is much “noise” from many sources, which you have to eliminate or take into account. What they found was that there always remained a background corresponding to a absolute temperature of 3.5 Kelvin. It did not matter which part of the sky they pointed the horn to, and whether it was day or night, there was always this background. They even cleaned the inside of the horn, removing pigeon droppings!

When the two teams came together, the solution was immediately clear. Penzias and Wilson had inadvertently discovered the Cosmic Microwave Background radiation, predicted by Dicke and his team. “Well, boys, we’ve been scooped “, Dicke supposedly said.

The two groups decided to write separate articles for the Astrophysical Journal of 1965, referring to each other. Cosmic Black-Body Radiation by Dicke, Peebles et al. and , very modestly titled, A Measurement of Excess Antenna Temperature at 4080 Mc/s by Penzias and Wilson.

In 1978 Penzias and Wilson received the Nobel Prize for Physics “for their discovery of cosmic microwave background radiation” Of course many in the scientific community found that the Nobel Prize should have been awarded to both teams. But (old fashioned) Nobel Prize rules made that impossible, teams can not get the Nobel Prize, only individuals (maximum three).

Roll and Wilkinson continued with their experiment and published the results the next year in the Physical Review Letters: ” Cosmic Background Radiation at 3.2 cm-Support for Cosmic Black-Body Radiation. Searching information for this post, I found a fascinating article, written a few weeks ago by Peter Roll, now retired of course, about his perspective on the 1965 discovery of the CMB. VERY readable, also for non-physicists.

I have written in some detail about the discovery of the CMB radiation because the importance of this discovery can hardly be overestimated. It changed the Big Bang theory from a controversial hypothesis into the standard model for the evolution of the universe. Here is another very readable article in Physics Today, one year after the discovery: A Bang, not a Whimper?

Of course there were still many questions. If the radiation was really thermal, it should have a well-defined spectrum. And it was of course very convincing that the radiation was the same at each point of the sky, but actually there should be minuscule differences, how else could stars and galaxies have formed, if the early universe was completely homogeneous?

The best way to investigate these questions, was to launch a spacecraft and observe the radiation outside Earth’s atmosphere. And that’s what happened. In 1974 NASA asked for scientific proposals and in 1989 the Cosmic Background Explorer (COBE) was launched. Two main experiments, FIRAS by John Mather, to determine the spectrum of the CMB radiation and DMR by George Smoot to measure the miniscule differences (the “anisotropy”) of the CMB.

Here is the spacecraft. Dimensions (without solar panels) ~ 4,5 x 2,5 m. The experiments are indicated, the Dewar contained liquid helium to cool especially FIRAS to near absolute zero temperature.

Here are the results. The CMB spectrum fits so perfectly the shape of a thermal source (“blackbody”) that it received a standing ovation when it was presented to the American Astronomical Society in January 1990.

The temperature of the CMB is 2.728 K, but Smoot found indeed tiny differences, depending on the location in the sky. Here is a map of the sky, with the temperature differences indicated in red (slightly warmer) and blue (slightly colder). When these results were published in 1992, they were frontpage news in the New York Times and Stephen Hawking in an interview called it “the greatest discovery of the century, if not of all times”.

In 2006 Mather and Smoot received the Nobel Prize for Physics “for their discovery of the blackbody form and anisotropy of the cosmic microwave background radiation”

Through the CMB we are looking back to the very young universe, 380.000 year old, before stars and galaxies were formed. Exploring these temperature differences, may help us to understand the evolution of the universe. But then a more detailed map of this anisotropy is needed!

In 2001 the Wilkinson Microwave Anisotropy Probe (WMAP) was launched. Until 2009 data have been collected, resulting in maps like this one, much more detailed.

And in 2009 the Planck observatory was launched. The instruments on board were cooled until 0.1 Kelvin, making it the coldest object in the universe..:-) Here is the Planck map, even more detailed.

You may wonder about the shape of these maps. It is called the Mollweide projection and it minimises the distortion you always get when you project a sphere on a plane. For comparison, here is the Mollweide projection of Earth.

There are two other discoveries in cosmology during the past 50 years that I have to mention, before I can finally come back to Jim Peebles and his Nobel Prize 🙂

The first one was the discovery of Dark Matter. In the 70s the American astronomer Vera Rubin studied the rotation of galaxies like the Andromeda galaxy and found that the outer regions of the galaxies were rotating much faster than expected, based on the visible matter of the galaxy and Kepler’s laws. An explanation could be that galaxies are surrounded by a halo of invisible (“dark”) matter. The existence of this Dark Matter has been widely accepted by the scientific community, but we still do not know yet what it is. According to many physicists, she deserved a Nobel Prize for her research, but she never got it. Because she was a woman? She passed away in 2016, Nobel Prizes can not be awarded posthumously. Here is a necrology: Vera Rubin, invisible to the Nobel Committee.

The second discovery was made in the 90s by two teams of astronomers who were studying the expansion of the universe. The Big Bang theory predicted that the expansion would slow down, because of the force of gravity. The crucial question was: will this force be big enough to stop the expansion, followed by a contraction, ending in a Big Crunch, or will the expansion go on forever. The result of their research was shocking: the expansion is not slowing down, but accelerating! There must be a repulsive force, which was called Dark Energy. Also here we do not know what it is. In 2011 the leaders of the two teams were awarded the Physics Nobel Prize “for the discovery of the accelerating expansion of the Universe through observations of distant supernovae”. I wrote a blog about it: Physics Nobel Prize (2011).

So, what did Jim Peebles discover? Nothing actually, and that may have been a reason that he received the Nobel Prize so late in life (he is now 84 year old) as the Nobel Committee has a preference for (experimental) discoveries.

But Jim Peebles rightly deserves the Nobel Prize because he has been instrumental in developing the theoretical cosmological framework for what is called physical cosmology. In 1982 he published a groundbreaking article about a cosmological model with dark matter in it and in 1984 an article in which he added the cosmological constant Λ (now called dark energy) to his model. This model , the Λ CDM  model, is at present the standard model of cosmology. For this work Peebles could (should) have been awarded the Nobel Prize many decades ago! Well, better late than never 🙂

With this Λ CDM model, using the properties of the CMB radiation and other experimental results, it is possible to determine how much normal matter, dark matter and dark energy there is in the Universe. The best fit to the (Planck) CMB data is obtained with the following values:

  • Atomic matter 4.9 %
  • Dark Matter 26.8 %
  • Dark Energy 68.3 %

Probably most of you will have seen this result. Everything we observe around us, our earth, the sun, the planets, the galaxies, it is only ~ 5% of our universe. About the other 95% we know basically nothing. Astonishing and mind-boggling.

Let me finish this post with two images. Below is an overview of the Big Bang expansion. The CMB is seen to the left, called the Afterglow Light Pattern. To the left you see “Inflation” and “Quantum Fluctuations”. The present theory is that in the first ~ 10−32 (!) second, the universe expanded exponentially. I don’t feel qualified to write a post about it, see the Inflation article in Wikipedia.

When the universe became transparent after 380.000 year, there were no stars and galaxies yet, the universe was dark, except for the afterglow! It took hundred millions of years, before the first stars were formed. More info in Wikipedia’s Chronology of the universe.

In 1980 Peebles published a book Large-Scale Structure of the Universe and that has always been his primary interest. There are about 200 billion galaxies in the observable universe, are they just randomly distributed? The answer is no, they are part of what nowadays is called the Cosmic Web. They are concentrated along filaments, with huge voids in between. In this artist impression, each light dot is a galaxy. Another mind-boggling image. 🙂 .

In 2013 I have written a post : Largest Structure in the Universe discovered, very readable if I may say so 🙂

APPENDIX

How is it possible to extract the values for dark matter, dark energy etc from a map of the sky with minuscule temperature differences?

The first step is to “translate” the temperature differences into what is called a power spectrum. The CMB map has cold and warm patches in various sizes. A power spectrum gives the intensity of these patches as function from their (angular) size.

Here is the power spectrum of the PLanck CMB map. The largest temperature fluctuations are found in patches of around 1 degree. Notice that the angular scale runs from left (large patches) to right (small patches). The red dots come from the CMB map. The green line is the best fit from the Λ CDM model, using the parameters given above.

Here is an instructive video, how the different parts of the power spectrum correspond from left to right to increasingly detailed structures.

The calculations are complex and need powerful computers.

In this simulation: Build a Universe you can play around with the various parameters. To run it on your computer, you need to have Flash installed. Not everybody will have Flash, so I have taken two screenshots. The first one, shows the “fit” for a universe with only normal matter. The second one uses parameters like given above.